![[LogoShip]](logo5.png)
Software for Windows
Science with your Sound Card!
Features:
Oscilloscope
Spectrum Analyzer
8-Channel
Signal Generator
(Absolutely FREE!)
Spectrogram
Pitch Tracker
Pitch-to-MIDI
DaqMusiq Generator
(Free Music... Forever!)
Engine Simulator
LCR Meter
Remote Operation
DC Measurements
True RMS Voltmeter
Sound Level Meter
Frequency Counter
Period
Event
Spectral Event
Temperature
Pressure
MHz Frequencies
Data Logger
Waveform Averager
Histogram
Post-Stimulus Time
Histogram (PSTH)
THD Meter
IMD Meter
Precision Phase Meter
Pulse Meter
Macro System
Multi-Trace Arrays
Trigger Controls
Auto-Calibration
Spectral Peak Track
Spectrum Limit Testing
Direct-to-Disk Recording
Accessibility
Data Logger
Waveform Averager
Histogram
Post-Stimulus Time
Histogram (PSTH)
THD Meter
IMD Meter
Precision Phase Meter
Pulse Meter
Macro System
Multi-Trace Arrays
Trigger Controls
Auto-Calibration
Spectral Peak Track
Spectrum Limit Testing
Direct-to-Disk Recording
Accessibility
Applications:
Frequency response
Distortion measurement
Speech and music
Microphone calibration
Loudspeaker test
Auditory phenomena
Musical instrument tuning
Animal sound
Evoked potentials
Rotating machinery
Automotive
Product test
Contact us about
your application!
Sound Card Missing Fundamental Mini-App
- Introduction
- Overview of the Mini-App
- Initial Set-Up and Calibration
- Two-Tone Experiments
- Continuous Tone Operation
- Play Music Operation
- Auditory Theories
- Phase Experiments
- External References and Links
- Buf0 Macro Array Memory Usage
- Missing_Fundamental Macro Listing
- _Miss_Fund_Ctrls Macro Listing
- _Miss_Fund_Update Macro Listing
- _Miss_Fund_Mtr Macro Listing
- _Miss_Fund_Crest Macro Listing
- _Miss_Fund_CF_Core Macro Listing
Introduction:
The Missing_Fundamental macro mini-app is included with Daqarta. It demonstrates the extent to which the brain perceives the fundamental frequency of a harmonic series of tones, even if that fundamental is not present.
For example, a tone complex consisting of only 220, 330, and 440 Hz sine-wave components may nevertheless be heard as 110 Hz. This is the greatest common divisor of the component frequencies, making it the most likely candidate for the missing fundamental, with the component tones thus representing the 2nd, 3rd, and 4th harmonics.
Determining whether you are hearing the fundamental or just the harmonics can be tricky. Researchers do this by presenting sequential pairs of tone complexes with different harmonic structures. Pairing the tones like this allows quick A-B comparisons: Does the second tone sound higher or lower than the first?
In the Missing_Fundamental mini-app, the first (A) tone complex is on for 300 ms, immediately followed by 300 ms of the B tone, then 400 ms of silence for a 1-second overall cycle which repeats indefinitely.
The default parameters result in the following A and B tones, where N gives the harmonic number; notice that both A and B have the same top frequency of 550 Hz, but for A it is the 5th harmonic of the (missing) fundamental of 110 Hz, while for B it is the 6th harmonic of 91.667 Hz (also missing, as is the 2nd harmonic at 183.333 Hz):
The spectrogram shows this graphically, with the missing components added as dotted lines:
You should note that besides the identical top frequencies, all of the other components that are actually present in the B tone are higher than those in the A tone. Yet for most people the B tone sounds definitely lower in pitch, because of the lower fundamental frequency that is implied by the harmonics.
Different parameters can yield different results. Just raising everything by 4 octaves (by setting the Fundamental control from 110 to 1760 Hz) can cause the apparent high-low sequence to reverse to low-high.
It turns out that there are innate differences between individuals regarding how readily they perceive the missing fundamental, as opposed to the lowest tone actually present (or any sort of average). Certain parameter combinations can highlight these differences. The Missing Fundamental mini-app allows you to change the effective fundamental frequency, the lowest harmonic to be included, the total number of harmonics, and the harmonic spacing.
This two-tone protocol is an extension of that used by researchers who showed that these individual differences in missing fundamental perception reflect measurable brain differences. (See the Schneider, Sluming, et. al. entry in the External References and Links section, below, for the full citation and a link to the PDF of this paper.)
The researchers studied the relative left- and right-hemisphere sizes of a brain structure called the lateral Heschl's gyrus (lHG) that is known to be involved in pitch detection. The left lHG was larger and showed stronger electrical responses than the right lHG in subjects who tended to hear the missing fundamental, whereas the opposite was true for those who tended to hear just the tones that were actually present.
Interestingly, their tests included many musicians, but there was no correlation of these differences with musical ability. The musicians had larger lHGs overall, but missing fundamental detection correlated only with the left-right assymetry, not absolute size... just the same as for non-musicians with their smaller lHGs.
The Missing Fundamental mini-app allows you to duplicate any tone pair from the above experiments exactly, including level calibration.
It does not, however, attempt to present specific sequences of tone pairs; it either presents the same tone pair repeatedly until you change the settings, or else it optionally steps through a range of fundamental frequencies with all other settings held constant.
You are not limited to the tones of the original study; your explorations can cover a wider frequency range, or use entirely different harmonic numbers. In particular, you can explore the effects of relative harmonic phase, and hence periodicity, on the perception of the missing fundamental. See the Phase Experiments subtopic for more information.
Overview of the Mini-App:
To run Missing_Fundamental, hit the F8 key followed by the unshifted f key. Note that this macro ID is case-sensitive because the FFT Filter macro uses an uppercase F as its ID.
Alternatively, hit CTRL+F8 to open the Macro Dialog and double-click on Missing_Fundamental in the Macro List.
Missing_Fundamental uses a Custom Controls dialog that allows adjustment of various parameters. You can open this Help topic by right-clicking anywhere in the dialog:
The Fundamental, Hz control defaults to 110 Hz. This is the value used as the fundamental for the harmonic series, even when that fundamental itself is not present, as in the default Fundamental OFF button state. The default Two-Tone Mode uses the Fundamental value directly in creating the first (A) tone of the two-tone pair. The second (B) tone is derived from A based upon other control settings, as described below under the 1-Harmonic A-B Increment button.
Lowest Harmonic Number defaults to 2. This means that the A harmonic series begins with the 2nd harmonic, which is twice the Fundamental value.
Total Harmonics defaults to 4. This total includes only the harmonics of one tone (A or B), and does not include the fundamental (if present). In the default case with Lowest Harmonic Number at 2, Fundamental at 110 Hz, and Fundamental OFF, the A tone will consist of harmonics 2 through 5, at 220, 330, 440, and 550 Hz.
The Missing_Fundamental mini-app uses one stream of the Daqarta Generator per tone component, whether A or B, harmonic or fundamental. The Generator has 8 streams, so the Total Harmonics default of 4 is the maximum you can set in Two-Tone mode. If you try to exceed that it will be forced back to 4, with a message: "4 Harmonics MAX in Two-Tone mode."
1-Harmonic A-B Increment indicates that the lowest harmonic of the B tone will be 1 harmonic number higher than the A tone. (You can set this increment from 1-4 via repeated clicks on the button. After 4, the next click will return to 1. You can move in the reverse direction by holding down the SHIFT key while you click the button. This multi-click operation is used with several of the other buttons, discussed below.)
The B tone will use the same Total Harmonics as A, so instead of running 2 through 5 the default B harmonics will run from 3 through 6. However, the frequency of the top B harmonic is always set to match that of the top A harmonic, or 550 Hz in this case. So if 550 Hz is the 6th B harmonic, then the (missing) fundamental must be 550 / 6 = 91.667 Hz, the 3rd will be 275, the 4th will be 366.667, the 5th will be 458.333, and of course the 6th will be 550.
The Show Values button allows you to display these on a resizeable custom meter. Note that crest factor (CF) values are only shown in Waveform Display mode:
The Fundamental OFF button can be clicked to Fundamental ON, but only if Total Harmonics is 3 or less in Two-Tone mode, due to the above-mentioned 8-voice limit. Otherwise the click will skip to Fundamental ONLY. The ON and ONLY conditions are just for quick reference, not normally part of a test.
An additional click past ONLY takes you to Fundamental OFF, STEP, which will step all frequencies up by 2 semitones (1/6 octave) after each two-tone pair. After 12 steps (24 semitones or two octaves), the cycle repeats. This allows you to quickly tell if there are perceptual flips from high-low to low-high, or vice-versa. The Show Values display is updated at each step, so you can note the frequency range of any changes.
The Calibrate Level button is discussed under the Initial Set-Up and Calibration subtopic, below.
The default Waveform Display mode triggers only on the B wave, so you will see a rolling waveform while the A tone is sounding, then a stable B waveform. You can hit Pause (or use ALT+P) to freeze the waveform while either A or B is visible, such as to save it to a file or a memory array, but only B will trigger at a repeatable point.
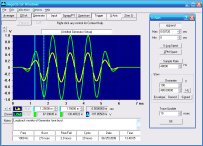
Here's a comparison of B waveforms with Fundamental OFF and Fundamental ON, using the default settings except with Total Harmonics reduced to 3. It was created by hitting Pause when each B waveform was visible, then saving each to the Juxt Trace Memory Array and adjusting the Spacing and Offset with the Array display on. The main Daqarta window was then copied to the Windows clipboard with ALT+PrintScreen, and pasted into Windows Paint for cropping and adding colored text labels:
Notice that the waveform is very similar between Fundamental OFF and Fundamental ON. In particular, note that both waveforms have the same period between the highest peaks: 11.364 ms, corresponding to the 88 Hz frequency of the B fundamental, even though that fundamental isn't really present in the OFF case. This observation features prominently in some proposed explanations of how the auditory system is able to perceive the missing fundamental. See the Auditory Theories subtopic, below.
The Zero Phase button indicates that all harmonics are aligned in time with their fundamental. This produces the large waveform peaks shown above. Repeated clicks of this button advance it through +/- Phase Factor (which enables the Phase Factor control), then Minimum-Peak Phases, and finally Random Phases (which enables the Randomize Phase button below it). All of these are discussed under the separate Phase Experiments subtopic.
If you click Waveform Display it will advance to Spectrum Display. The spectrum will be shown with X-log and Y-log axes, with Decimate active using a Decimate Factor automatically selected (along with X-Axis eXpand) to give best resolution of the spectral peaks. This image was created as for the waveform display above, but with no Spacing or Offset of the traces:
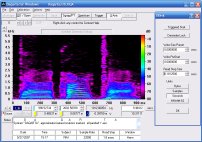
A second click will advance to Spectrogram Display, again with optimized Decimate Factor and eXpand settings. Since spectrograms can't be superimposed to show the differences between Fundamental OFF and ON, this image just shows the OFF condition for both A and B tone complexes of the original default 4-harmonic tones:
Spectrum Window is active in Spectrum Display and Spectrogram Display by default. This is usually the best option because it reduces the "skirts" around the spectral peaks. However, it does make the tips slightly wider. You can use ALT+W to toggle the Window off for sharper peaks, especially in Spectrogram mode, at the expense of trash due to the increased skirt amplitudes.
The default Two-Tone Mode allows up to 4 harmonics with a missing fundamental, or 3 plus the fundamental, on each tone complex. Alternatively, you can click the Two-Tone Mode button to Continuous Tone (described in detail under its own subtopic) that allows up to 7 Total Harmonics (plus the fundamental, with Fundamental ON) in a single ongoing tone complex.
Holding down the ALT key while clicking the Two-Tone / Continuous button takes you to Play Music mode. This disables all other controls in the mini-app and starts a DaqMusiq MIDI rendition of "Frere Jacques" called MissFundamental.DQM. The song (melody only) is played with 8 sine-wave voices, one per harmonic, including the fundamental through the 8th. This allows you to toggle the fundamental and/or any of the harmonics off and on during the performance. See the separate Play Music Operation subtopic.
Initial Set-Up and Calibration:
Once you start the Missing_Fundamental mini-app, the very first thing you should do is adjust the volume. (The F9 key opens Daqarta's volume slider dialog.) Whether you are listening with headphones or speakers, it is important to avoid overdriving your system. Without changing any settings in Missing_Fundamental, adjust the volume for a comfortable listening level. Then see if the tone quality (timbre) changes suddenly as you reduce the volume. If so, your system was distorting on the higher level, so keep it below that.
The study by Schneider, Sluming, et.al. used sound levels that were 50 dB above the listener's detection threshold. (See the External References and Links section, below, for the full citation and a link to the PDF of this paper.)
If you want to duplicate that, click the Calibrate Level button. The digital level of the generated signal (before the output DAC) will be reduced by 50 dB, to 10^(-50 / 20) = 0.00316 = 0.316% of the normal level.
The Daqarta volume control dialog will open and a message will appear:
"Adjust volume until you can just
detect the tones, then toggle Calibrate
off for 50 dB SL Two-Tone test."
The volume control acts on the analog output stream after the DAC, so when you set the analog volume such that you can just detect the signal, then restore the pre-DAC digital level, the overall sound level will be 50 dB higher than your detection threshold.
Note that the digital level of 0.316% means that the signal is using less than 7 bits of the 16-bit DAC range. There will be more distortion during this step... roughly 100 times more, in fact, or about 1% overall. But since you are adjusting the volume such that you can barely hear the signal, that 1% distortion will be about 40 dB below your detection threshold so you will not be able to hear it.
Note also that your hearing is naturally more sensitive in some ranges than others, with the most sensitive region being around 1000 Hz and falling off above or below that. So if you calibrate at 110 Hz and test at (say) 880 Hz, the sound will be louder (ie. more than 50 dB above your 880 Hz threshold).
It's not clear how Schneider, Sluming, et. al. calibrated to get their 50 dB levels, but the important thing for your own research is to keep track of whatever approach you use so that you can repeat it as needed.
Two-Tone Experiments:
As noted in the Introduction, with the default parameters most people hear the A-to-B transition as high-to-low, even though the B component frequencies are actually higher than those in A (except for the identical top frequencies).
But you may hear the transition as the opposite direction. Regardless of which way you hear it, the direction may change at higher or lower Fundamental settings. Try moving it in octave steps: 27.5, 55, 110, 220, 440, 880, 1760 Hz.
Once you find a frequency with the opposite direction, try searching back to find exactly where the change takes place. You will probably find there is a large range where your impression of the direction is ambiguous; sometimes it's one way, sometimes the other.
Often the perceived direction depends on the path you take to get there. For example, the author usually perceives the default 110 Hz setup as definitely high-low. Raising it to 220 Hz gives a definite low-high direction, at least when listening through headphones at moderate levels. But going back to 110 and working up in 10 Hz steps yields high-low the whole way, to 220 Hz and beyond. This phenomenon may be like viewing reversing in-out Necker cubes, or a photo of lunar craters, where the preferred direction can change; once you get conditioned to a certain direction it tends to persist.
Level-Dependent Effects:
Sometimes a very slight change in listening conditions can prompt a direction change. When listening to the above 220 Hz setup with headphones and hearing a definite low-high direction, even a slight reduction in volume caused it to revert back to high-low... often as small as 1-2 dB, after a preliminary hunt established the threshold region (about 6 dB louder than the 50 dB level obtained by Calibrate Level).
Near the level threshold there seems to be a strong psychological component to the direction change. When above the threshold level and stepping downward, for example, sometimes the direction changed as expected even when the level did not. (To do this type of test yourself, have an assistant change, or not change, the volume while you listen without being able to see what's actually happening.)
What causes this level-dependent effect? Consider that with a 220 Hz fundamental the upper components are near or above 1000 Hz, where they are not well-separated by the auditory system. If the missing fundamental can't be clearly determined, the system might be expected to respond to just the average component frequencies. This would give a low-high direction.
Notice that the louder condition gives low-high and the softer gives high-low. This implies that even when the components are louder, and presumably clearer due to being farther above any background noise, they are nonetheless not separated.
Intermodulation distortion (IMD) can cause difference or combination tones that are not present in the original signal. Note that this distortion can take place in the sound card amplifier, the headphones, or even your ears. Since the component tones are at harmonic numbers that differ by 1 (such as the 4th and 5th for the A tone), the difference tone will be exactly at the fundamental frequency.
Most forms of distortion produce stronger distortion products at higher levels, but that would tend to make the missing fundamental more detectable, leading to a high-low direction instead of the actual low-high.
However, crossover distortion can create IMD in amplifiers (but not headphones or ears). By its nature crossover distortion is actually worse at lower levels. (See Sound Card Distortion - Theory And Measurement for details.) That might explain why the missing fundamental is more detectable at lower levels. How can you tell?
Daqarta's IMD Meter mini-app can measure intermodulation distortion. A loopback cable from the headphone output back to the line input would allow measurement of the IMD in the headphone amplifier. If it rises sharply as the volume is lowered into the region of the high-low direction, you might count that as evidence for crossover being the culprit.
But there is a much simpler test: At the higher level where the low-high direction is heard, just move the headphones away from your ears. (This may be easier with on- or over-the-ear instead of in-the-ear phones.) This reduces the volume of the sound to your ears without changing the amplifer level, so there is no distortion change. If the direction switches to high-low, it proves that amplifier distortion is not to blame. That's exactly what happened in the author's tests.
The remaining possibility is that the phenomenon is due to something in the auditory system itself. One likely suspect is the fact that the tuning sharpness of auditory filters is worse at high levels, so reducing the level could increase the ability of the system to discriminate the individual components and thus determine the missing fundamental.
But curiously, the low-high direction at 220 Hz switches back to high-low by about 300 Hz... and raising the level doesn't bring back low-high. By around 1000 Hz the low-high response has returned at high levels, with high-low at low levels. Above 1200 Hz it is always low-high regardless of level.
More research is clearly needed!
Frequency Range Tests:
As noted in the Overview section, the Harmonic A-B Increment controls the lowest B harmonic number relative to the Lowest Harmonic Number setting, which applies to A. The harmonic numbers increase in steps of one above that, until the Total Harmonics value is reached. The increment can be set from 1-4, which with the other settings at their defaults gives these harmonic numbers and frequencies:
Harmonic A-B Increment
--- 1 ---- --- 2 ---- --- 3 ---- --- 4 ----
A5 550 B6 550 B7 550 B8 550 B9 550
A4 440 B5 458.33 B6 471.43 B7 481.25 B8 488.89
A3 330 B4 366.67 B5 392.86 B6 423.50 B7 427.78
A2 220 B3 275 B4 314.29 B5 343.75 B6 366.67
A1 (110) - - - -
B1 (91.67) - - -
B1 (78.57) - -
B1 (68.75) -
B1 (61.11)
Notice that as the Increment increases, all of the component frequencies increase as well (except the constant top frequency), but the missing fundamental decreases.
The Lowest Harmonic Number, as noted above, applies to the A tone. It can be set from 2 to 16. If you set it to 4, with Total Harmonics reduced to 2, the Harmonic A-B Increment at 2, and the Fundamental at 332.2 Hz you will get the following:
A5 1661 B7 1661 A4 1328.8 B6 1423.7 ... ... A1 (332.2) B1 (237.3)
This is a close approximation of the two-tone test found on the Steve Mould - Science Presenter site under "Audio Illusion: Do you hear the missing fundamental?" (See the External References and Links section, below.) The actual tone frequencies were not published on the site; these were obtained by analyzing the spectrum with Daqarta.
As-is, this seems to give a good split between those who hear it as high-low and those who hear low-high.
This general setup also makes a good test for overall sensitivity to frequency range. Try setting Fundamental back to the 110 Hz default, then toggling Show Values on. Now click the Fundamental OFF button 3 times, past ON and ONLY to Fundamental OFF, STEP.
Now the top frequency will step from 550 Hz (5 times 110) to 2200 Hz (2 octaves higher, or 20 times 110) in 12 steps. For the author, the direction starts out as definitely high-low, but when the top passes 1100 Hz (A missing fundamental of 220 Hz and B of 157 Hz) the perception changes to low-high.
Advancing the Harmonic A-B Increment from 2 to 3 and then to 4 makes the initial high-low effect even more pronounced.
Even more surprising, with Fundamental set to (say) 80 Hz the first few steps are low-high. But when the A fundamental crosses 110 Hz (top over 550 Hz) the direction switches to high-low, then when it passes about 220 Hz (top over 1100 Hz) it changes back to low-high, as above. For the author, this behavior seems to be essentially the same with any Harmonic A-B Increment settings.
Two-Tone Macro Parameters:
Some of the parameters for Two-Tone Mode are preset in the macro script, instead of having adjustable controls. These parameters set the timing of the two-tone cycle, as well the order of A and B presentation, the application of phase changes, the harmonic spacing, waveform type, and the number of frequency steps and range of the Fundamental OFF, STEP mode.
All of these are set at the start of the Missing_Fundamental macro script; you can easily change them by single-clicking on Missing_Fundamental in the Macro List, then clicking the Edit button to view the script, and editing the Definition directly. Here is the start of the script:
;<Help=H4913 R=15m ;Rise/Fall times for A/B two-tone test H=300m ;On (High) time per tone G=0 ;Gap between A and B tones (none) C=1000m ;Cycle time for 2 tones plus silence QX=0 ;QX=1 to eXchange A,B order to B,A QP=2 ;Phase change only on B (1=A, 3=both) U1=1 ;A harmonic increment U2=1 ;B harmonic increment UW=0 ;0=Sine, 1=Tri, 2=Ramp, 3=Sqr, 4=Pulse W=4 ;Sweep limit freq = W times fundamental QN=12 ;Frequency steps in above sweep range
The cycle-timing parameters R, H, G and C are in seconds, so R=15m (note the 'm') means that the Rise (and Fall) times are 15 msec each. These 4 parameters specify a different default cycle timing from the one used by Schneider, Sluming, et.al. (See the External References and Links section, below, for the full citation and a link to the PDF of this paper.)
The timing they used would be:
;<Help=H4913 R=10m ;Rise/Fall times for A/B two-tone test H=500m ;On (High) time per tone G=250m ;Gap between A and B tones C=1500m ;Cycle time for 2 tones plus silence
However, they repeated the tone pair only once (A, B, A, B) then waited 2 seconds during which the subject indicated whether the pitch seemed to move from low to high or high to low. The tone parameters were then changed for the next test.
The Lowest Harmonic Number in their tests was either 2, 3, 4, or 7. When they used 2 or 3, the equivalent Harmonic A-B Increment was 1. When they used 4 or 7 it was 2. Thus, their lowest A-to-B harmonic number transitions were always one of:
2 -> 3
3 -> 4
4 -> 6
7 -> 9
The Missing_Fundamental mini-app allows you to set the Lowest Harmonic Number from 2 to 16, and the Harmonic A-B Increment from 1 to 4.
Within the tones of either A or B, the harmonics in Schneider, Sluming, et.al. always incremented in steps of 1, as set here via the default U1=1 for A and U2=1 for B. You can experiment with larger steps for one or both.
You can change QX=0 to QX=1 to reverse the A,B order to B,A.
Schneider, Sluming, et.al. did not investigate phase as a parameter. This mini-app allows you to apply phase changes as selected by advancing the Zero Phases button and using the Phase Factor control or Randomize Phase button. You can apply these changes to either or both A and B tone complexes as set via parameter QP. The default here is QP=2 to only apply phase changes to B; you can use QP=1 to apply them only to A or QP=3 to apply them to both. See the separate Phase Experiments subtopic below for more information.
The UW=0 control sets the default waveform for each harmonic to Sine. The possible options you may wish to experiment with are:
UW=0 Sine
UW=1 Triangle
UW=2 Ramp
UW=3 Square
UW=4 Pulse
Note that the Ramp and Pulse waveforms normally allow you to change settings such as ramp slope or pulse widths for each stream (each harmonic, in this case). Here they are fixed such that in Ramp mode each component rises slowly and drops abruptly, and in Pulse mode the pulse is positive for 1/8 of a cycle, then negative for 1/8, then zero for the remainder.
W=4 and QN=12 control the frequency steps in Fundamental OFF, STEP mode. W sets the upper limit of the fundamental, as a factor to be multiplied by the current Fundamental frequency. So in the default case with Fundamental set to 110 Hz and W=4, the maximum fundamental (on the last step) will be 440 Hz, or a 2 octave increase.
QN=12 sets the number of steps above the initial Fundamental setting. The steps are exponential, so in the default case where W=4 (2 octaves) each step will be 1/6 octave or 2 semitones.
These parameters are also used in Continuous Tone mode for Fundamental OFF, SWEEP operation, but they behave somewhat differently since that uses a continuous frequency sweep instead of discrete steps. The total sweep duration is QN * C seconds, which in the default case will be 12 * 1000 msec = 12 seconds. W still sets the maximum frequency as above, so the sweep would run from 110 Hz to 440 Hz in 12 seconds. The sweep moves at an exponential rate such that the time for the first octave (110 to 220 Hz) would take 6 seconds, the same as the second (220 to 440 Hz).
Continuous Tone Operation:
Clicking the default Two-Tone Mode button toggles to Continuous Tone. This mode allows up to 7 Total Harmonics, even with Fundamental ON.
The 1-4 Harmonic A-B Increment button changes to 1-4 Harmonic Increments, and now controls the spacing between harmonics in the single continous tone. When set to 1, with Lowest Harmonic Number set to 2, the harmonic series will be (1), 2, 3, 4, etc. With Harmonic Increments set to 2 it would be (1), 2, 6, 8, etc.
The Calibrate Level button changes to Levels EQUAL, and can be toggled to Levels 1/N. The latter means that the amplitude of each component is proportional to the reciprocal of its harmonic number. Besides whatever effects this might have on the missing fundamental phenomenon, it also allows nice demonstrations of waveform synthesis from sine wave components. With Fundamental ON, Lowest Harmonic Number set to 2, and Harmonic Increments set to 1, the tone will consist of all harmonics up to the limit set by Total Harmonics, falling off at 1/N. This will approximate a ramp waveform. Increasing Total Harmonics will sharpen it.
Toggling back to Fundamental OFF and increasing Harmonic Increments to 2 will also give a ramp wave, but at twice the frequency. Increasing Lowest Harmonic Number to 3 and Harmonic Increments to 3 will give a ramp at 3 times the frequency, while setting these both to 4 will give 4 times the frequency. Toggle Show Values on to see what's going on.
Likewise, with Fundamental ON, Lowest Harmonic Number set to 3, and Harmonic Increments set to 2, the tone will consist of only odd harmonics falling off at 1/N, which will approximate a square wave.
With Fundamental OFF, Lowest at 2, and Increments at 4, you get a square wave at twice the frequency.
Clicking Fundamental OFF advances it to Fundamental ON and then to Fundamental ONLY, just as for Two-Tone Mode, but the next click is Fundamental OFF, SWEEP (instead of STEP).
As noted in Two-Tone Macro Parameters, the SWEEP mode for Continuous Tone performs a continuous exponential frequency sweep from the Fundamental frequency to 4 times that frequency (two octaves), over an interval of 12 seconds. You can change the time and frequency range factor via the same macro parameters that control STEP operation in Two-Tone Mode. You can monitor the current frequency values via Show Values, and you can see them graphically by clicking the Waveform Display button to Spectrum Display or Spectrogram Display.
With Continuous Tone mode it is more difficult to be sure you are actually hearing a missing fundamental, since there are no separate A and B tones to compare.
Set Total Harmonics to 7. Listen carefully as you move back and forth between OFF, ON, and ONLY conditions, and notice that the tonal quality doesn't change much from OFF to ON; both cases are much more strident than the pure sine wave of the ONLY condition.
At this point you may be thinking that since the OFF condition (harmonics without fundamental) sounds so little like the ONLY condition (just the fundamental), how can it be claimed that it is somehow inducing a perception of the "missing" fundamental? Wouldn't it be more correct to simply say that when the harmonics are present, they dominate the perception?
To get a better sense of the origin of the claim, try going to the ONLY state and reducing the Fundamental frequency from 110 Hz down to 55 (musical A1). Your speaker system or headphones will need good bass response for you to hear this well. You should notice a periodic pulsing or fluttering quality to the sound, possibly felt as much as heard, as if you were hearing and feeling the individual waveform peaks passing like blades on a fan.
Now when you add the harmonics (Fundamental OFF or ON), you will hear this same "periodicity" effect in either case, at the same rate you hear in the ONLY condition.
Caution: The harmonics-present conditions will sound much louder, even though they have less than half the RMS level of the fundamental alone. (Toggle the Voltmeter on with the ALT+V keys to see this.) This is because our ears are not as sensitive at low frequencies, but hear the higher harmonics much better.
The astute observer will notice that the same periodicity is visible in the Fundamental OFF and ON waveform displays... in fact they look almost identical (displaced vertically here for clarity):
This leads to the natural assumption that the ear is somehow analyzing the waveform and detecting the periodicity. But things are not completely straightforward, as discussed in the Auditory Theories subtopic.
Play Music Operation:
You may have heard about the missing fundamental effect being used musically to play notes that are lower than ordinary instruments can create... or even lower than humans can actually hear. The Play Music mode allows you to experiment with this.
Holding down the ALT key while clicking the button marked Two-Tone Mode or Continuous Tone takes you to Play Music, which will cause all other Missing_Fundamental controls to be disabled until you click on the button again (with or without ALT).
In Play Music the display is set to Pitch Track (in the Sgram/PT control dialog), and Pitch-to-MIDI is activated after loading a DaqMusiq MIDI setup called MissFundamental.DQM. This setup plays a rendition of "Frere Jacques" with 8 sine-wave voices, one each for the fundamental plus harmonics 2 through 8. These voices play the melody only, without the original chords used in the Frere Jacques setup.
The Instrument for each voice is set to Ocarina, which creates a clean sine wave tone when played by the standard Microsoft GS Wavetable synthesizer. This is important so that each voice will be a simple harmonic of the fundamental.
Clicking the Instrument On/Off (Ocarina) button of a voice allows you to toggle the fundamental (voice 1) or any harmonic 2-8 off and back on again at will while the song plays. (Caution: The voices all stay in sync as long as at least one is active; if you toggle all 8 off you may have trouble getting them back in sync. If so, just toggle the Pitch-to-MIDI On/Off button off and back on.)
You may find that this is all rather anti-climactic, since the song just sounds a bit thinner or less robust without the fundamental. The effect may be a lot more compelling when used to create really low notes with an orchestra or a pipe organ. That's because, besides our ears, we sense low notes with our whole body. Since the waveform created will have the periodicity of the missing fundamental, there will be peaks and dips in air pressure (as well as seat and floor vibrations) at the fundamental frequency, which we can feel directly.
If you want to explore this, you can shift the entire song to a lower range. To do that, open the Voice 1 Setup dialog by clicking on that button. Then delete the leading semicolon from the first line of the script, so that it reads n9=-12. That will shift everything down by one octave (12 semitones).
The first note of the fundamental will change from B2 at 123.471 Hz to B1 at 61.735 Hz. This will be hard to hear among the other harmonics playing, both because our ears are less sensitive at lower frequencies, and also because speakers (and headphones) are less sensitive as well. So you might very well not detect a difference when you toggle the fundamental off. But that doesn't really prove you are hearing the missing fundamental, it might just indicate that you can't hear the fundamental in any case.
To prove you are hearing a missing fundamental you can toggle Voice 1 off, along with all voices except Voice 2. Now start toggling the higher-numbered voices on; if you hear lower pitches than with Voice 2 alone, it must be due to the missing fundamental effect. This works even with inexpensive headphones; it's typically a rumbling, growling sound compared to the clean 2nd harmonic with Voice 2 alone.
If you change the first line to n9=-24 everything goes down by 2 octaves, so the first note will be B0 at 30.868 Hz. Using n9=-36 will take it down by 3 octaves to B-1 at 15.434 Hz.
Auditory Theories:
The mystery of the missing fundamental is that we are hearing something that is "not really there"... or is it? Consider a tone complex consisting of a fundamental at 88 Hz, plus harmonics 3 through 5 (at 264, 352, and 440 Hz, respectively). Compare it to the same case without the fundamental, only the harmonics:
There is a definite periodicity in both waveforms at the 88 Hz fundamental period (11.364 msec), even when that component isn't there, as shown by the Spectrum Display view of the same tones:
So it seems obvious that the auditory system must be detecting this waveform periodicity, and we expect that this should be simple to do... after all, we can see the periodicity with our eyes!
But nothing about the auditory system is simple. The main issue it has to solve is that neurons, which ultimately must convey to the brain anything we can hear, are much too slow to handle the full frequency range of normal sounds. The ear solves this with a divide-and-conquer approach using many neurons in parallel, each handling only a tiny sliver of the total frequency range.
Sound enters the fluid-filled spiral cochlea (from the Greek for "snail") as a pressure wave that excites the basilar membrane, which due to its tapering width (and mass and stiffness) vibrates at different locations for different sound frequencies. The pattern of vibration looks roughly like the spectrum seen above.
All along the length of the basilar membrane are sensory inner hair cells (IHCs) that detect the vibration at each location. Motion causes an IHC to excite fibers running to neurons in the cochlear nucleus. When a neuron fires, it creates a train of constant-amplitude spikes, with the firing rate proportional to the amplitude of the motion at the IHC's frequency-specific location.
This is illustrated below, where the violet waveform represents a varying-amplitude sine wave at the specific frequency of an IHC. The green spike train has a constant amplitude, but its spike rate is proportional to the sound amplitude:
At another sound frequency this neuron might fire only rarely, since the basilar membrane would not vibrate at this particular IHC position. But another IHC would be excited instead, producing spikes on its own dedicated neuron.
Each sound frequency thus has a separate neural pathway that sends its amplitude to the brain, so it doesn't need to send frequency information... the frequency is encoded by the position of the IHC and hence its particular output neuron. This is called the place principle, or sometimes the labeled line theory.
Think of a piano, where there are separate keys for each note. All keys behave basically the same, each key mechanism (IHC) conveying only information about how hard it has been hit (amplitude) to the mechanical linkage (neuron to brain) that eventually results in sound production (perception). The basic pitch of the sound is determined by which key is hit, not by how hard it is hit.
The above spectrum has only 512 frequency positions, while the ear has about 3500 IHCs to provide much finer frequency resolution. At the low frequencies in the above missing fundamental example, the filtering is so selective that each harmonic would excite a different IHC, corresponding to the distinct peaks in the spectrum. This sharp filtering means that each IHC would see a near-sinusoidal waveform, not the total multi-component waveform with periodicity corresponding to the missing fundamental. The IHC tuned to the fundamental frequency would thus only be excited when that frequency was actually present.
But without the periodicity, how could the brain perceive a missing fundamental?
In principle, some sort of mechanical distortion in the excitation of the basilar membrane could cause a distortion product at the missing fundamental frequency. This explanation was ruled out by experiments conducted over 60 years ago. Masking noise was introduced that would have overwhelmed any such distortion product, yet perception of the missing fundamental was not blocked.
However, even without waveform periodicity, the place principle alone can, in many circumstances, explain the missing fundamental through pattern recognition... something the brain excels at. Consider that the auditory system, with a separate neural pathway for each pitch it can detect, is similar to the visual system with a separate pathway from each retinal cell for each image pixel the eye can detect. The visual system can recognize the letter 'A', for example, even when much of it is missing:
The brain learns to associate a certain pattern of neural activity with a certain shape or sound. It can then make that same association even if the pattern isn't complete, as long as certain critical elements are present.
This place or spectral theory explanation is fairly well accepted for low frequencies, as in our example here. However, it has difficulties explaining certain observations, such as listeners that can hear the missing fundamental even when only a few upper harmonics are present that are so high in frequency that they are not well separated by the cochlear filtering process.
Also, the missing fundamental effect can be changed by manipulating the relative phases of the harmonics. This changes the waveform peaks but does not affect the spectrum, so presumably would not be detectable via place theory. (See the Phase Experiments subtopic.)
These and other auditory phenomena point toward a temporal theory, which uses waveform periodicity.
But wait, didn't we lose that periodicity information when the sound was filtered into separate neurons for each frequency? Well, not quite. If each neuron encodes the phase of the frequency component along with its amplitude, there is theoretically enough information for the brain to reconstruct the original waveform, including its periodicity. This is similar to the way an inverse Fourier transform can reconstruct a waveform from a spectrum.
It turns out that this phase information is indeed preserved to a large extent, although in a statistical fashion. As noted, the firing rate of each neuron encodes the amplitude of the filtered input waveform, but the maximum firing rate is much too low to encode the complete filtered IHC waveform, which is itself in the same frequency range. In fact, it's even too low to fire once per cycle in many cases.
But when the neuron is able to fire at all, it tends to fire at a peak in the incoming IHC waveform; if it can't respond to the current peak, it responds to the next one, or the one after that. The average firing rate would thus be some sub-multiple of the true IHC input frequency, but it would still be phase locked with respect to the IHC sine wave.
If the brain can keep track of the relative phase across neuron outputs for multiple harmonics, it might be able to reconstruct the original overall waveform, and hence determine the period.
One signal processing technique that can determine the period from the overall waveform is known as autocorrelation. Computationally, this typically requires an array of time delays, although no such structures have yet been identified in the auditory system.
In the case of poorly-separated ("unresolved") upper harmonics, a single IHC is exposed to multiple harmonics. It thus sees a waveform with peaks at the same period as the fundamental, and its neural output would thus show that periodicity.
This is essentially the same phenomenon as auditory "beats" when only two components are present. You can explore this by setting Total Harmonics to 2 and setting Fundamental and Lowest Harmonic so that their product is in the 1000 Hz range or above. You might want to set Continuous Tone mode to get clean waveform triggering.
The lowest Fundamental frequency you can set this way is 10 Hz. Alternatively, the Monaural and Binaural Beats (Beats_Demo) mini-app allows you to set its Difference Frequency (which is equivalent to the missing fundamental) as low as you want, although it is limited on the high end to 100 Hz. Click the Mode: Binaural button to Mode: Monaural. Set the Center Frequency to 1000 Hz and the Difference Frequency as desired.
With either of the above approaches (but especially with Beats_Demo), note that at very low "beat" or "fundamental" frequencies, such as a few hertz, you perceive waveform periodicity as discrete, countable events. At 10 Hz the beat rate is just barely countable, but if you go much beyond that it becomes "roughness", and as you go higher still it eventually becomes a true pitch. If you move the Center Frequency or Lowest Harmonic down to more-typical musical ranges and repeat the above, you'll notice that the roughness is more likely to be heard as a deep fundamental... a gut-rumbling super-low organ note, for example.
This may indicate that beats, roughness, and the missing fundamental are all part of the same general phenomenon, which would point to a temporal theory. The current consensus seems to be that both spectral and temporal theories are involved. The paper on lateral Heschl's gyrus by Schneider, Sluming, et.al. reports that they "found a strong neural basis of both types of pitch perception, which corroborated the functional specialization of left auditory cortex for rapid temporal and the right hemisphere for spectral processing." (See the External References and Links section, below, for the full citation and a link to the PDF of this paper.)
Phase Experiments:
The above Auditory Theories section discusses two different ways the missing fundamental might be detected by the ear-brain system. The place (spectral) theory would seem to require only the presence of the harmonic component frequencies at their respective spectral positions on the basilar membrane; the temporal theory would seem to require detectable waveform peaks. The available evidence indicates both processes contribute to the phenomenon.
One approach that might shed information on the contributions of each type of process is to manipulate the relative phases of the individual components to maximize or minimize waveform peaks.
Assuming the individual components are well-separated on the basilar membrane, the sharp tuning should insure that phase does not affect the amplitude of vibration at the location of any frequency component. If so, place-based processing should not be affected by relative phase shifts.
On the other hand, since phase changes can affect the size and placement of waveform peaks, we expect they might affect temporal processing.
Zero Phase:
The Missing Fundamental mini-app has a phase mode button that defaults to Zero Phase. In this mode all harmonics start at the same phase and thus produce strong peaks in the overall waveform at the missing fundamental periodicity.
The relative "peakiness" is given by the crest factor (CF), which is the ratio of the peak amplitude to the RMS average over one waveform period. Show Values reports CF values as dB, shown beneath the harmonic lists for each tone in Waveform Display mode only. For the default parameters at Zero Phase, the CF for the A tone is 8.022 dB and for the B tone it is 8.410 dB:
When you change any parameter you will notice that the Show Values display is updated immediately, including the CF for tone A, but the B CF vanishes briefly and is updated with the new value a moment later. That's because these CFs are actual measured values, and the _Miss_Fund_Crest task must wait for the B tone to sound before it can be measured.
+/- Phase Factor:
Clicking Zero Phase button to +/- Phase Factor enables the Phase Factor, deg/N control. This applies the specified phase shift (45 degrees default) times the harmonic number to each B component (or to all, in Continuous Tone mode), with the sign alternating between positive on even harmonics and negative on odd. In the default case with Fundamental OFF and the B tone having harmonics 3-6 the phase is:
N Hz Deg
5A 550.000 0.000
4A 440.000 0.000
3A 330.000 0.000
2A 220.000 0.000
1A (110.000) 0.000
CF 8.022 dB
6B 550.000 0.000
5B 458.333 270.000
4B 366.667 0.000
3B 275.000 90.000
1B (91.667) 0.000
CF 5.044 dB
The default of 45 degrees per harmonic gives the lowest B crest factor with the default parameters; this will still hold true if you change the Fundamental frequency, but not if you change Lowest Harmonic Number or Total Harmonics, or toggle Fundamental OFF to Fundamental ON, or change Harmonic A-B Increment.
In general, you should start at 45 and slowly work down while watching the CF for tone B. CF values are not shown in Fundamental ONLY mode. They are also not shown in Fundamental OFF, STEP mode, but in that case they are the same as the default Fundamental OFF mode since the only thing changing is the fundamental frequency.
Note that since the A and B tones use the same top harmonic component (550 Hz here), Phase Factor can't apply the computed phase directly to B without changing A. Instead, it forces the top phase to zero (to match the A tone) and adjusts all the lower harmonics (and the fundamental, if Fundamental ON is active) to have the same relative phases as computed by the above relationship. The resulting waveform is identical, just shifted in time. (No such adjustment is needed in Continuous Tone mode since there is no shared harmonic.)
Below is the resulting waveform, compared to the default Zero Phase. There is a substantial reduction in peakiness of the Phase Factor waveform. Although not shown, the spectra and spectrograms of the two are identical. However, to the author's ears, the default Zero Phase has a strong high-low pitch drop, while the Phase Factor version is a mild low-high pitch rise. (This effect may be best heard on headphones.)
You can toggle back and forth to compare; to go back to Zero Phase, hold down the SHIFT key while clicking the Phase Factor button. Then release the SHIFT key while clicking to return to Phase Factor.
This directional change seems to indicate that periodicity plays a role in at least some conditions, with some observers. There is plenty of territory to explore here; this might be fruitful area for a science fair project, undergraduate thesis, or graduate research.
See also the Phase Audibility Demonstration mini-app for related experiments.
Minimum-Peak Phases:
If you click Phase Factor again it advances to Minimum-Peak Phases. This mode applies the Newman algorithm discussed in Multitone Signals with Low Crest Factor by Boyd. (See External References and Links, below.) Although this may be an optimal algorithm for signals with many tones that form a gap-free harmonic series, it is usually not as good as the above +/-Phase Factor method for missing fundamentals with small numbers of harmonics as used here. The Minimum-Peak method gives a CF of 6.030 dB for the B tone with default parameters, compared to 5.044 dB for Phase Factor as seen above.
It is even worse with Total Harmonics reduced to 3 and Fundamental ON, giving a CF of 8.572 dB compared to 5.053 for the best Phase Factor of 34 deg/N.
In Continuous Tone mode, however, with Total Harmonics set to 7 (maximum) and Lowest at 2 with Fundamental ON to form an unbroken series from 1 to 8, it gives a CF of 5.413 dB; slightly besting the optimum Phase Factor CF of 5.687 dB with Factor at 44 deg / N.
If you have a different algorithm you'd like to use, you can replace the Newman formula. See Custom Phase Algorithm, below.
Random Phases:
Another click on the phase button moves from Minimum-Peak to Random Phases, which also enables the Randomize Phase button below it). Random Phases sets the phases of the B components to pseudo-random values, which were stored as an array of constants when the Missing_Fundamental macro started up.
The array can be replaced with a new set of random values by clicking Randomize Phase; otherwise, the same values are used whenever Random Phases is active. This allows you to compare a particular set of random phases with any of the other phase modes.
The pseudo-random number generator seed that is used to create the random phases is stored in VarP, which is saved across Daqarta sessions. This value is set when you hit Randomize Phase. It is used to set the seed for the default random phases created when Missing_Fundamental starts. This means that if you find a set of random phases that you want to keep using, you will be able to use them in future sessions as long as you do not hit Randomize Phase.
If you want to try other random phases, but still be able to return to a prior set, you need to save the seed. One way to do that would be to modify _Miss_Fund_Ctrls by uncommenting the Field1 line:
IF.Ctrls=9
VarP=Posn?r
; Field1=VarP(0)
Now when you find a seed you want to save, you can copy Field1 and paste it into a Windows Notepad file, or you can save up to about 200 seeds in Daqarta's Notes for later copy to a final destination.
Although it may seem like Zero Phase always gives the largest crest factor (largest waveform peaks), that isn't the case. A few minutes spent clicking the Randomize button should demonstrate that you can get up to about 1 dB higher CF, especially with Fundamental OFF.
Custom Phase Algorithm:
If you have (or are developing) an algorithm for picking phases, you can replace the Newman approach used for Minimum-Peak Phases. There are 3 places the Newman formula is used in Miss_Fund_Update: for the A tone (if QP = 1 or 3 near the start of Missing Fundamental, for the B tone, and for Continuous Tone mode. The latter code is simplest:
IF.Btn3=2
P=(180 * (UH - 1)^2 / UN) % 360
ENDIF.
Here UH is the harmonic number, UN is the total number of harmonics plus the fundamental (if Fundamental ON), and the computed phase P is in degrees. (The % 360 modulus operation at the end is not part of the original algorithm; it just keeps results in a manageable 0-360 degree range for display purposes.) Note that the fundamental (UH = 1) phase is always 0.
The A and B tones are complicated by the need to force both top harmonics to 0, since a single Generator stream (R.3) is used for both. This involves using the Newman algorithm to compute the phase Q for each top harmonic (which will be different since A and B have different top harmonic numbers, even though the frequencies are the same). Q is the phase that would have been used for this harmonic according to the formula, but since we will be forcing this to 0 it must be used to compensate each lower harmonic phase P.
The correction factor is the ratio of the lower harmonic number over the top harmonic number, times Q.
For the A tone, the code is:
IF.UP=2
Q=180 * (Buf0[8] - 1)^2 / UN
P=((180 * (UA - 1)^2 / UN) - UA / Buf0[8] * Q) % 360
ENDIF.
Here Buf0[8] holds the top harmonic number and UA is the current harmonic number whose phase is being computed.
The B tone code is similar, except the top harmonic number is in Buf0[9] and UB is the current harmonic number:
IF.UP=2
Q=180 * (Buf0[9] - 1)^2 / UN
P=((180 * (UB - 1)^2 / UN) - UB / Buf0[9] * Q) % 360
ENDIF.
You only need to replace the B code if you are working exclusively in Two-Tone mode.
Specific Phase Values:
Alternatively, if you have specific phases you want to use, you can replace the array of random values used by the Random Phases option. Do this in the main Missing_Fundamental code, right after the part where the array is filled:
Posn#r=VarP
QI=0
WHILE.QI=<8
Buf0[QI]=rnd(0,360)
QI=QI+1
WEND.
This is where the random values are set into Buf0[0] to Buf0[7] for later use by Random Phases. You can leave this intact and just insert your new code right after it, overwriting the pre-set values.
Your added code will look like this, but with your values replacing the 350, etc:
Buf0[3]=350.000 ;5B Buf0[2]=240.000 ;4B Buf0[1]=130.000 ;3B
The above assumes you are using Lowest Harmonic = 2, Total Harmonic = 4, and 1-Harmonic A-B Increment settings (defaults). In this case, the top B harmonic will be 6B; the top harmonic phase in Two-Tone mode is always 0, so you don't set anything for that component.
If you reduce Total Harmonics to 3, only 4B and 3B (Buf0[2] and Buf0[1]) need to be set this way; the top harmonic will be 5B, but will automatically use 0 instead of Buf0[3]. Fundamental ON will always use Buf0[0] as the random 1B phase.
If you increase Lowest Harmonic to 3, all the above harmonic numbers will increase to match. Note that 'Lowest' refers to the A harmonics; the lowest B harmonic will be higher by the Harmonic A-B Increment. If the Increment is 1, then the B harmonics will run from 4 to 7 instead of 3 to 6, but the Buf0 indices are unchanged: Buf0[3] is still the next-to-highest as long as Total = 4.
If you have modified the QB=2 line near the start of Missing_Fundamental to allow phase changes to apply to A only (QB=1) or to both A and B (QB=3), and you want to set specific Random Phases values for A, the comparable Buf0 index values are 7, 6, and 5. The A fundamental is always on Buf0[4] when Fundamental ON is active.
Random Phases can also be applied to Continuous Tone mode. With Lowest = 2, and Total = 7, the harmonics run from 2 to 8 and the corresponding Buf0 indices run from 0 to 6. Buf0[7] is never used in Continuous mode; if Fundamental ON is active, it is always set to 0 phase.
External References and Links:
Research Papers:
Schneider, P., Sluming, V., Roberts, N., Scherg, M., Goebel,
R., Specht, H., Dosch, H.G., Bleeck, S., Stippich, C., Rupp,
A., "Structural and functional asymmetry of lateral
Heschl's gyrus reflects pitch perception preference".
Nature Neuroscience, volume 8, number 9, September 2005,
pages 1241-1247.
Download PDF
Boyd, S., Multitone Signals with Low Crest Factor,
IEEE Transactions On Circuits And Systems, volume CAS-33,
number 10, October 1986, pages 1018-1022.
Download PDF
Newman, D., An L1 Extremal Problem For Polynomials,
Proc. Amer. Math. Soc., volume 16, Dec 1965, pages
1287-1290.
Download PDF
Steve Mould - Science Presenter:
Audio Illusion: Do you hear the missing fundamental?
Note: The original is no longer available at: <http://stevemould.com/audio-illusion-hear-missing-fundamental/>. An archived copy is available at: <https://web.archive.org/web/20180918182437/http://stevemould.com/audio-illusion-hear-missing-fundamental/>. However, the sound doesn't seem to be working.
Wikipedia:
Buf0 Macro Array Memory Usage:
Index Use
0-7 Random harmonic phases
8 A top harmonic number
9 B top harmonic number
10-17 Continous tone harmonic numbers
19 B fundamental frequency
20-24 A harmonic numbers
25-29 B harmonic numbers
30-37 Continuous tone harmonic phases
40-44 A harmonic phases
45-48 B harmonic phases
50 Crest factor task status
51 A crest factor, dB
52 B crest factor, dB
53 Continuous tone CF, dB
57 Btn7 prior state save during Play Music
58 Btn7 single-time Play Music tip flag
100-103 "-Harmonic A-B Increment" text string
104-107 "-Harmonic Increments" text string
900-999 Buf0#Bs=9 Block Save during Play Music
Missing_Fundamental Macro Listing:
;<Help=H4913 R=15m ;Rise/Fall times for A/B two-tone test H=300m ;On (High) time per tone G=0 ;Gap between A and B tones C=1000m ;Cycle time for 2 tones plus silence QX=0 ;QX=1 to eXchange A,B order to B,A QP=2 ;Phase change only on B (1=A, 3=both) U1=1 ;A harmonic increment U2=1 ;B harmonic increment UW=0 ;0=Sine, 1=Tri, 2=Ramp, 3=Sqr, 4=Pulse W=4 ;Sweep limit freq = W times fundamental QN=12 ;Frequency steps in above sweep range Close= ;Close any open data file Decimate=0 ;Decimate off Sgram=0 ;Spectrogram off PitchTrk=0 ;Pitch Track off Spect=0 ;Spectrum off Xpand=0 ;No X-axis expand SpectWindOn=1 ;Spectrum window on E.IF.Input= ;If Input is enabled, Input=0 ;Force Input off ENDIF. TrigMode=GenSync ;Set to Generator sync Trig=1 ;Trigger on TraceUpdate=10 ;10 ms per trace update A.LoadGEN="MissFund" ;Load Generator setup, no prompt Ctrls="<<Missing Fundamental" ;Custom Controls dialog title Ctrl0="<<Fundamental, Hz" ;Ctrl0 title Ctrl0="<S(10,4000)" ;Slider, 10-4000 Hz Ctrl0="<p(3)" ;3 decimal places Ctrl0=110 ;110 Hz default Ctrl1="<<Lowest Harmonic Number" Ctrl1="<S(2,16)" ;Lowest harmonic 2-16 Ctrl1="<p(0)" Ctrl1=2 ;2nd harmonic default Ctrl2="<<Phase Factor, deg/N" Ctrl2="<S(0,360)" Ctrl2="<D" ;Disable, Btn3 enables Ctrl2=45 ;45 degrees/harmonic Ctrl3="<<Total Harmonics" Ctrl3="<S(1,7)" ;Allow 1-7 harmonics Ctrl3="<p(0)" Ctrl3=4 ;4 default Btn0="Fundamental OFF" Btn0="<M(3)" ;Multi-state button, 0-3 Btn0=0 ;Default = OFF Q0=0 ;Saves prior state for reverse Buf0[100]#a4="-Harmonic A-B Increment" ;Label tail, default 2-tone mode Buf0[104]#a4="-Harmonic Increments" ;Label tail, Continuous mode Btn1="1" + Buf0[100](a4) ;"1-Harmonic A-B Increments" default Btn1="<M(3)" ;1,2,3,4-harmonic increments Btn1=0 ;Default to 1- Btn2="Calibrate Level" ;Changes to Equal vs 1/N if Continuous Btn2="<T" ;Simple on/off Toggle button Btn2=0 ;Default to off (two-tone) Q2=0 ;Default to Equal for Continuous M=1 ;Level factor, reduced for Calibrate Btn3="Zero Phases" Btn3="<M(3)" ;Multi-state button, 0-3 Btn3=0 Btn4="Show Values" ;Toggles meter display Btn4="<T" Btn4=0 Btn5="Randomize Phase" Btn5="<M" ;Momentary pushbutton Btn5="<D" ;Disable, Btn3 enables when Random Btn5=0 Btn6="Waveform Display" ;Toggle to Spectrum or Spectrogram Btn6="<M(2)" ;Multi-state button, 0-2 Btn6=0 Btn7="Two-Tone Mode" ;Toggle to Continuous or Music Btn7="<M(2)" ;Multi-state button, 0-2 Btn7=0 Buf0[57]=0 ;Saves prior state during Music Buf0[58]=0 ;Set to 1 after Play Music tip IF.UW=>0 ;Wave other than default Sine? IF.UW=>4 ;Limit to 4=Pulse max UW=4 ENDIF. UI=0 ;Start with Stream 0 = L.0. WHILE.UI=<8 ;Set all 8 streams to new Wave Ch=UI ;Stream (channel) number Ch.Wave=UW ;Set Wave type for stream UI=UI+1 ;Next stream WEND. ENDIF. K=2*R + H + G ;Min Burst Cycle time IF.C=<2 * K ;2 bursts / overall cycle C C=2 * K ;Increase C as needed ENDIF. IF.QX=0 ;Default A,B burst order? A=0 ;A starts with no Lag B=K ;B starts after A complete QA="A" ;Label for 1st burst QB="B" ;Label for 2nd burst ELSE. ;Else reverse B,A order B=0 ;B starts with no Lag A=K ;A starts after B complete QA="B" ;1st burst called "B" QB="A" ;2nd burst called "A" ENDIF. UI=0 WHILE.UI=<7 ;Set streams 0-6 Ch=UI ;Stream (channel) number Ch.BurstRise=R Ch.BurstHigh=H Ch.BurstFall=R IF.UI=<4 ;Streams 0-3 are 2nd burst Ch.BurstLag=B ELSE. ;Streams 4-6 are 1st burst Ch.BurstLag=A ENDIF. Ch.BurstCycle=C ;Total Cycle for each burst Ch.TrainCycle=C UI=UI+1 WEND. R.3.BurstLag=0 ;Stream 7 is double burst, no Lag R.3.BurstRise=R R.3.BurstHigh=H R.3.BurstFall=R R.3.BurstCycle=K ;Set each burst cycle to min R.3.TrainLag=0 R.3.TrainCount=2 ;2 bursts per train R.3.TrainCycle=C ;Overall 2-burst train cycle Gen=1 ;Start sound RO.Disp=0 ;No Right Out display (=Left) Posn#r=VarP ;Repeatable random seed QI=0 WHILE.QI=<8 Buf0[QI]=rnd(0,360) ;8 random phases in Buf0 QI=QI+1 WEND. Mtr0="<<Harmonic Components" ;Mtr0 title Mtr0="<C(ColorNum?l)" ;Mtr0 text color of Left Out Mtr0="<B(ColorNum?S)" ;Background color of screen Mtr0="<F(30)" ;30-pixel default font height Mtr0="<f(3)" ;Lucida Console font family @_Miss_Fund_Ctrls=Ctrls ;Set Custom Controls macro Task="-_Miss_Fund_Mtr" ;Remove Mtr0 task Task="-_Miss_Fund_Crest" ;Remove crest factor task IF.Buf0[57]=>1 ;Play Music active? PitchMIDI=0 ;Stop playing if so PitchMIDIdlg=0 ;Close Pitch-to-MIDI dialog PitchTrk=0 ;Stop pitch tracking SgramDlg=0 ;Close Sgram/PT dialog Gen=1 ;Gen on for RO.Disp re-enable ENDIF. RO.Disp=1 ;Restore Right Out display Decimate=0 ;Decimate off, if on Sgram=0 ;Spectrogram off, if on Spect=0 ;Spectrum off, back to waveform Trig=1 ;Trigger on Gen=0 ;Generator off on exit Msg= ;Remove 2-tone CAL message Msg="<<" Mtr0= ;Meter off Mtr0="<f(2)" ;Arial font family
_Miss_Fund_Ctrls Macro Listing:
;<Help=H4913 IF.(2 * Btn7 + Btn2)=!1 ;If not 2-tone CAL mode, Msg= ;Remove calibration message Msg="<<" ENDIF. IF.Ctrls=0 ;Ctrl0 = Fundamental freq? @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=1 ;Ctrl1 = Lowest Harmonic? Ctrl1=cint(Ctrl1) ;Convert to integer @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=2 ;Ctrl2 = Phase Factor? @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=3 ;Ctrl3 = Total Harmonics? Ctrl3=cint(Ctrl3) ;Convert to integer IF.Btn7=0 ;Two-tone mode? IF.Ctrl3=>4 ;Limit to 4 harmonics max Ctrl3=4 Msg="<<Too Many Harmonics!" Msg="4 Harmonics MAX in Two-Tone mode." ENDIF. IF.Ctrl3=4 ;If 4-harmonic two-tone, IF.Btn0=1 ;No 'Fundamental ON' Btn0=0 Btn0="Fundamental OFF" ENDIF. ENDIF. ENDIF. @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=4 ;Btn0 = Fundamental OFF, ON, etc? TrigMode=GenSync IF.Btn0=1 ;If ON attempted IF.(!Btn7 && int(Ctrl3>>2))=1 ;In 4 harmonic 2-tone mode IF.Q0=0 ;Prior = OFF? (normal) Btn0=2 ;Ahead to ONLY ELSE. ;Prior = ONLY (w.SHIFT) Btn0=0 ;Back to OFF ENDIF. ELSE. ;Else set Level in _Update Btn0="Fundamental ON" ENDIF ENDIF. IF.Btn0=0 ;If OFF, Btn0="Fundamental OFF" L.0.Level=0 ;Set Level to 0 ENDIF. IF.Btn0=2 ;If ONLY, Btn0="Fundamental ONLY" L.0.Level=100 ;Set Level to 100% ENDIF. IF.Btn0=3 ;STEP / SWEEP mode? TrigMode=Norm IF.Btn7=1 ;Continuous tones? Btn0="Fundamental OFF, SWEEP" ELSE. ;Else 2-tone burst mode Btn0="Fundamental OFF, STEP" ENDIF. Task="_Miss_Fund_Mtr" ;Meter task tracks progress ELSE. Task="-_Miss_Fund_Mtr" ;Else meter change on Update ENDIF. Q0=Btn0 ;Save for prior state if SHIFT @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=5 ;Btn 1 = Harmonic Increment? UH=Btn1+1 ;Harmonic number 1-4 Btn1="" + UH + Buf0[100 + 4 * Btn7](a4) ;Label Btn1 @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=6 ;Btn2 = Calibrate / Level? IF.Btn7=1 ;Continuous tone mode? IF.Btn2=0 Btn2="Levels EQUAL" ELSE. Btn2="Levels 1 / N" ENDIF. Q2=Btn2 ELSE. ;Calibrate if 2-tone mode IF.Btn2=0 ;If calibrate off, M=1 ;Level factor = 1 ELSE. ;Else calibrate ON M=10^(-50/20) ;Factor = -50 dB GenVolDlg=1 ;Show F9 volume ctrls Msg="<<Level Calibration:" Msg="Adjust volume until you can just" _ +n + "detect the tones, then toggle Calibrate" _ +n + "off for 50 dB SL Two-Tone test." ENDIF. ENDIF. @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=7 ;Btn3 = Phase Mode? IF.Btn3=0 ;Set all phases to 0? Btn3="Zero Phases" Ctrl2="<D" ;Disable Phase Factor Btn5="<D" ;Disable Randomize Phase ENDIF. IF.Btn3=1 ;Phase Factor? Btn3="+/- Phase Factor" Ctrl2="<N" ;Enable control Btn5="<D" ;Disable Randomize Phase ENDIF. IF.Btn3=2 ;Minimum phase? Btn3="Minimum-Peak Phases" Ctrl2="<D" ;Disable Phase Factor Btn5="<D" ;Disable Randomize Phase ENDIF. IF.Btn3=3 ;Random Phases? Btn3="Random Phases" Ctrl2="<D" ;Disable Phase Factor Btn5="<N" ;Enable Randomize Phase ENDIF. @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=8 ;Btn4 = Show Values? Mtr0= ;Clear meter display IF.Btn4=0 ;Show Values now OFF? Task="-_Miss_Fund_Crest" ;Remove crest factor task ELSE. ;Else Show Values is ON Buf0[50]=3 ;Block crest factor updates Task="_Miss_Fund_Crest" ;Install crest factor task Mtr0="<H4913" ;Set Meter Help to enable @_Miss_Fund_Update ;Update waves (and meter) ENDIF. ENDIF. IF.Ctrls=9 ;Btn5 = Randomize Phase? VarP=Posn?r ;Save random seed ; Field1=VarP(0) ;Copy to Field1 QI=0 WHILE.QI=<8 ;For each of 8 components Buf0[QI]=rnd(0,360) ;Set random 0-360 deg QI=QI+1 WEND. @_Miss_Fund_Update ;Update waves (and meter) ENDIF. IF.Ctrls=10 ;Btn6 = Waveform/Spectrum/Sgram IF.Btn6=0 Btn6="Waveform Display" Trig=1 Decimate=0 Spect=0 Sgram=0 ENDIF. IF.Btn6=1 Btn6="Spectrum Display" Trig=0 Spect=1 Ylog=1 Xlog=1 ENDIF. IF.Btn6=2 Btn6="Spectrogram Display" Trig=0 Sgram=1 Xpand=1 YlogTop=0 ;0 dB top color TraceMag=8 ;-40 dB range ENDIF. @_Miss_Fund_Update ENDIF. IF.Ctrls=11 ;Btn7 = Two-Tone/Continuous/Music? IF.Buf0[58]=0 ;Tip message given yet? Buf0[58]=1 ;Don't show it again Msg="<<TIP:" ;Title for message Msg="ALT+Click to Play Music" ENDIF. U7=Buf0[57] ;Prior Btn7 state before click IF.U7=>1 ;Was it Play Music? (2 or 3) Buf0[57]=U7 & 1 ;Back to 0 or 1 Btn7=Buf0[57] ;New Btn7 state Buf0#Br=9 ;Restore variables from Block 9 PitchMIDI=0 ;Stop playing PitchMIDIdlg=0 ;Close Pitch-to-MIDI dialog PitchTrk=0 ;Stop pitch tracking Sgram=0 ;Sgram/PT OFF SgramDlg=0 ;Close Sgram/PT dialog Gen=1 ;Generator ON IF.Btn6=0 ;Wave Display? Trig=1 ;Triggered if so ELSE. IF.Btn6=1 ;Spectrum? Spect=1 ELSE. ;Else Spectrogram Sgram=1 ENDIF. ENDIF. Ctrl0="<N" ;Enable other controls Ctrl1="<N" IF.Btn3=1 ;If Btn3 = Phase Factor Ctrl2="<N" ;Re-enable it ENDIF. Ctrl3="<N" Btn0="<N" Btn1="<N" Btn2="<N" Btn3="<N" Btn4="<N" IF.Btn3=3 ;If Btn3 = Random Phases Btn5="<N" ;Enable Randomize ENDIF. Btn6="<N" IF.Btn7=0 ;Replace "Play Music" label Btn7="Two-Tone Mode" ELSE. Btn7="Continuous Tone" ENDIF. @_Miss_Fund_Update ;Update waves (and meter) ELSE. ;Wasn't Play Music IF.Key?$=2 ;ALT-key down? Buf0[57]=U7 | 2 ;Set Play Music state Btn7=2 Buf0#Bs=9 ;Save variables to Block 9 Btn7="Play Music" ;Re-label button Mtr0= ;Remove meter display Gen=0 ;Generator OFF Trig=0 ;Trigger OFF Decimate=0 ;Decimate OFF Sgram=1 ;Sgram/PT ON SgramDlg=1 ;Show Sgram/PT dialog XpandMax=2531.25 ;Set vertical range XpandMin=46.875 Xpand=1 PitchShow=2 ;Show MIDI Note / Inst PitchWide=1 ;Show wide pitch track PitchYaxis=0 ;Show notes on Y axis PitchSteps=1 PitchMIDIdlg=1 ;Open Pitch-to-MIDI dialog A.LoadDQM="MissFundamental" ;Auto-load Daqmusiq setup PitchTrk=1 ;Start pitch tracking PitchMIDI=1 ;Start playing Ctrl0="<D" ;Disable all other controls Ctrl1="<D" Ctrl2="<D" Ctrl3="<D" Btn0="<D" Btn1="<D" Btn2="<D" Btn3="<D" Btn4="<D" Btn5="<D" Btn6="<D" ELSE. ;Toggle Two-Tone / Continous Buf0[57]=Buf0[57] # 1 ;Flip between 0 and 1 Btn7=Buf0[57] ;Set new button state IF.Btn7=0 ;Two-Tone mode? Btn7="Two-Tone Mode" ;Label button IF.Btn0=3 ;STEP or SWEEP mode? Btn0="Fundamental OFF, STEP" ;Use STEP for 2-tone ENDIF. IF.Ctrl3=>3 ;Total harmonics more than 3? Ctrl3=4 ;Limit to 4 max IF.Btn0=1 ;If Fundamental ON now, Btn0=0 ;Force it OFF Btn0="Fundamental OFF" ENDIF. ENDIF. Q2=Btn2 ;Save continuous Level state Btn2="Calibrate Level" ;Change button usage for 2-tone Btn2=0 ;Force Calibrate off M=1 ;Unity Level factor ELSE. ;Going to Continuous mode Btn7="Continuous Tone" ;Label button IF.Btn0=3 ;STEP or SWEEP mode? Btn0="Fundamental OFF, SWEEP" ;Use SWEEP for Continuous ENDIF. Btn2=Q2 ;Restore saved Level state IF.Q2=0 ;Set corresponding label Btn2="Levels EQUAL" ELSE. Btn2="Levels 1 / N" ENDIF. ENDIF. UH=Btn1+1 ;Harmonic number 1-4 Btn1="" + UH + Buf0[100 + 4 * Btn7](a4) ;Label Btn1 @_Miss_Fund_Update ;Update waves (and meter) ENDIF. ENDIF. ENDIF.
_Miss_Fund_Update Macro Listing:
;<Help=H4913 GenUpdate=0 ;No Generator restarts F=Ctrl0 * (Ctrl1 + Ctrl3 - 1) IF.Btn0=3 ;SWEEP / STEP mode? UN=Ctrl3 ;Total Harmonics, no fundamental UX=1 ;Will set Sweep on IF.Btn7=1 ;Continuous (not two-tone)? S=QN * C ;Sweep length = #steps * step time QX=0 ;No Stairs (continuous sweep) ELSE. ;Else two-tone mode S=C ;Sweep length for one step QX=QN ;Number of Stairs ENDIF. F=F * W ELSE. ;Else Fundamental OFF, ON, ONLY UN=Ctrl3 + Btn0 ;Total Harmonics + Fundamental if ON UX=0 ;No Sweep ENDIF. IF.Btn6=>0 ;Spectrum or Spectrogram display? X=cint(SmplRate / (F * 8)) IF.X=>1 Decimate=1 DecX=X ELSE. Decimate=0 ENDIF. XpandMax=1.2 * F ENDIF. UI=0 WHILE.UI=<8 ;Set Sweep paramters for all streams Ch=UI ;Set stream (channel) number Ch.Sweep=UX ;Sweep on/off Ch.SweepLength=S ;Duration Ch.SweepStairs=QX ;Number of stairs, else 0=continuous UI=UI+1 WEND. IF.Btn7=0 ;Default two-tone mode? UC=0 ;Meter update count UA=(Ctrl3 - 1) * U1 + Ctrl1 ;Top A harmonic # UB=(Ctrl3 - 1) * U2 + Ctrl1 + Btn1 + 1 ;Top B harmonic # Buf0[8]=UA Buf0[9]=UB B=Ctrl0 * UA / UB ;B fundamental freq Buf0[19]=B ;Store for meter IF.Btn0=2 ;Fundamentals ONLY? R.0.ToneFreq=Ctrl0 ;A params on Right 0 R.0.SweepEnd=Ctrl0 * W ;Fundamental * factor R.0.Level=100 R.0.Burst=1 L.0.ToneFreq=B ;B params on Left 0 L.0.SweepEnd=B * W L.0.Level=100 * M L.0.Burst=1 UI=1 WHILE.UI=<4 ;All upper streams off Ch=UI ;Left stream Ch.Level=0 Ch=UI + 4 ;Right stream Ch.Level=0 UI=UI + 1 WEND. ELSE. ;Else OFF, ON, or STEP UI=Ctrl3 ;Total A (or B) harmonics UJ=UI ;Default A loop index IF.Btn0=1 ;If Fundamental ON, UJ=UI+1 ;Include extra loop pass ENDIF. L=(100 / UN) * M ;100% / components * CAL factor Ch=7 IF.QP=2 ;Phase change only on B? UP=0 ;Zero phase here if so ELSE. ;Else 1 = A only, 3 = both UP=Btn3 ;Use Btn3 as-is ENDIF. WHILE.UJ=>0 ;Do total A (or B) harmonics IF.UI=0 ;Last pass (A Fundamental)? UA=1 ;Fund = "1st harmonic" Ch=4 ;Always R.0. channel ENDIF. F=Ctrl0 * UA ;Fundamental * harm number IF.Btn0=3 ;If STEP, UF=F * W ;Use max freq as limit ELSE. UF=F ;Else current freq ENDIF. IF.UF=<SmplRate/2 ;Freq in audible range? Ch.ToneFreq=F ;Set output freq if so Ch.SweepEnd=F * W ;End freq for STEP mode IF.UP=0 ;Zero phase? P=0 ;Set harmonic phase ENDIF. IF.UP=1 ;Phase Factor? US=1 - (Buf0[8] & 1) * 2 ;A top, alt sign Q=Ctrl2 * Buf0[8] * US ;A top phase = ref US=1 - (UA & 1) * 2 ;Harmonic alt sign P=(Ctrl2 * UA * US - UA / Buf0[8] * Q) % 360 ENDIF. IF.UP=2 ;Min Peak? Q=180 * (Buf0[8] - 1)^2 / UN ;Newman top phase P=((180 * (UA - 1)^2 / UN) - UA / Buf0[8] * Q) % 360 ENDIF. IF.UP=3 ;Random? IF.UA=Buf0[8] ;Top A harmonic? P=0 ;Phase = 0 ELSE. P=Buf0[UI+3] % 360 ;Pre-stored rand phase ENDIF. ENDIF. IF.P=<0 ;Neg phase? P=P + 360 ;Pos equivalent ENDIF. Ch.TonePhase=P ;Set output phase Buf0[40 + UI]=P ;Store phase for Mtr Buf0[20 + UI]=UA ;Store harmonic num Ch.Burst=1 ;Burst ON Ch.Level=L ;Set level ELSE. ;Else if freq too high, Ch.Level=0 ;Set to silence Buf0[20 + UI]=0 ;Store for Mtr ENDIF. UA=UA - U1 ;Next-lower harmonic Ch=Ch - 1 ;Next-lower stream UI=UI - 1 ;Next-lower harm index UJ=UJ - 1 ;Next-lower loop index WEND. ;Do all Total harmonics IF.Btn0=0 ;Fundamental OFF? Buf0[40]=0 ;Set phase = 0 ENDIF. UI=7 - Ctrl3 WHILE.UI=>3 ;If Total was less than 4... Ch=UI Ch.Burst=0 ;Set remaining to silence Ch.Level=0 UI=UI - 1 WEND. ;Do all A components Buf0[25 + Ctrl3]=UB ;Save B top harmonic number Buf0[45 + Ctrl3]=0 ;Phase always zero UI=Ctrl3 - 1 ;Top harm shared, no dup UJ=UI ;Default B loop index IF.Btn0=1 ;If Fundamental ON, UJ=UI + 1 ;Include extra loop pass ENDIF. UB=UB - U2 ;Next-lower harmonic num IF.QP=1 ;Phase change only on A? UP=0 ;Zero phase here if so ELSE. ;Else 2 = B only, 3 = both UP=Btn3 ;Use Btn3 as-is ENDIF. Ch=3 ;(Top - 1) harmonic stream WHILE.UJ=>0 ;Do total - 1 remaining harms IF.UI=0 ;Last pass (B Fundamental)? UB=1 ;Fund = "1st harmonic" Ch=0 ;Always L.0. channel ENDIF. F=B * UB ;Freq = B fund * harm num IF.Btn0=3 ;If STEP, UF=F * W ;Use max freq as limit ELSE. UF=F ;Else use current freq ENDIF. IF.UF=<SmplRate/2 ;Freq in audible range? Ch.ToneFreq=F ;Set output freq if so Ch.SweepEnd=F * W ;End freq for STEP mode IF.UP=0 ;Zero phase? P=0 ENDIF. IF.UP=1 ;Phase Factor? US=1 - (Buf0[9] & 1) * 2 ;Alternating top sign Q=Ctrl2 * Buf0[9] * US ;Top phase = ref US=1 - (UB & 1) * 2 ;Alt harmonic sign P=(Ctrl2 * UB * US - UB / Buf0[9] * Q) % 360 ENDIF. IF.UP=2 ;Min-Peak? Q=180 * (Buf0[9] - 1)^2 / UN ;Newman phase P=((180 * (UB - 1)^2 / UN) - UB / Buf0[9] * Q) % 360 ENDIF. IF.UP=3 ;Random? P=Buf0[UI] % 360 ;Pre-stored rand phase ENDIF. IF.P=<0 ;Neg phase? P=P + 360 ;Pos equivalent ENDIF. Ch.TonePhase=P ;Set output phase Buf0[45 + UI]=P ;Store phase for Mtr Buf0[25 + UI]=UB ;Store harmonic num Ch.Burst=1 ;Burst ON Ch.Level=L ;Set level ELSE. ;Else if freq too high, Ch.Level=0 ;Store for Mtr Buf0[25 + UI]=0 ;Set to silence ENDIF. UB=UB - U2 ;Next-lower harmonic Ch=Ch - 1 ;Next-lower stream UI=UI - 1 ;Next-lower harm index UJ=UJ - 1 ;Next-lower loop index WEND. ;Do all Total-1 harmonics IF.Btn0=0 ;Fundamental OFF? Buf0[45]=0 ;Set phase = 0 ENDIF. UI=4 - Ctrl3 ;Highest unused Left (B) stream WHILE.UI=>0 ;Set remaining to silence Ch=UI Ch.Burst=0 Ch.Level=0 UI=UI-1 WEND. L.0.ToneFreq=B L.0.Level=0 IF.Btn0=1 ;If Fundamental ON, L.0.SweepEnd=B * W ;Set B Fundamental L.0.Level=L ;End for STEP mode L.0.Burst=1 IF.Ctrl3=<4 ;If less than 4 harmonics, R.0.ToneFreq=Ctrl0 ;Set A fundamental also R.0.SweepEnd=Ctrl0 * W R.0.Level=L R.0.Burst=1 ENDIF. ENDIF. ENDIF. ELSE. L.0.ToneFreq=Ctrl0 ;Set fundamental freq L.0.TonePhase=0 ;And phase IF.Btn0=!2 ;If not Fundamental ONLY L.0.Burst=0 ;No Burst L=100 / UN ;100% / total components IF.Btn0=1 ;Fundamental ON? L.0.Level=L ;Set fundamental Level ELSE. L.0.Level=0 ;0 if OFF or SWEEP ENDIF. UI=Ctrl3 - 1 ;Total Harmonics - 1 WHILE.UI=>-1 ;Do all but Fundamental UH=(Btn1+1) * UI + Ctrl1 ;Harmonic number Ch=UI+1 ;Stream number Ch.Burst=0 ;No Burst F=UH * Ctrl0 ;Fundamental * Harmonic IF.Btn0=3 ;SWEEP mode? UF=F * W ;Max freq if so ELSE. UF=F ;Else static freq ENDIF. IF.UF=<SmplRate/2 ;If max freq in range Ch.ToneFreq=F ;Stream (start) freq Ch.SweepEnd=F * W ;Max (for SWEEP) IF.Btn3=0 ;Zero Phases? P=0 ENDIF. IF.Btn3=1 ;Phase Factor? US=1 - ((UI + Ctrl1) & 1) * 2 ;Sign P=Ctrl2 * UH * US ENDIF. IF.Btn3=2 ;Min-Peak Phases? P=(180 * (UH - 1)^2 / UN) % 360 ;Newman factor ENDIF. IF.Btn3=3 ;Random Phases? P=Buf0[UI] ;Pre-computed ENDIF. Buf0[10 + UI + 1]=UH ;Store harmonic num IF.P=<0 ;Neg phase? P=P + 360 ;Equiv. pos ENDIF. Ch.TonePhase=P ;Set stream phase Buf0[30 + UI + 1]=P ;Store for meter Ch.Level=L / UH^Btn2 ;Level EQUAL or 1/N ELSE. ;Max freq out of range Ch.Level=0 ;Prevent aliasing Buf0[10 + UI + 1]=0 ;Don't show it ENDIF. UI=UI - 1 ;Next-lower harm, stream WEND. UI=Ctrl3 + 1 ;Unused upper harmonics WHILE.UI=<8 Ch=UI Ch.Burst=0 ;Set to null Ch.Level=0 Buf0[10 + UI]=0 UI=UI + 1 WEND. ELSE. ;Fundamental ONLY L.0.Level=100 ;Max Level L.0.Burst=0 ;No Burst UI=1 ;Set all harmonics to null WHILE.UI=<8 Ch=UI Ch.Burst=0 Ch.Level=0 Buf0[10 + UI]=0 UI=UI + 1 WEND. ENDIF. ENDIF. UZ=0 ;Force meter update, if active Buf0[50]=0 ;Null crest factor state flag Buf0[51]=0 ;Null A crest factor Buf0[52]=0 ;Null B crest factor Buf0[53]=0 ;Null Continuous crest factor GenUpdate=3 ;Force Generator restart @_Miss_Fund_Mtr ;Do meter update as needed
_Miss_Fund_Mtr Macro Listing:
;<Help=H4913 IF.Btn4=1 ;Show Values? IF.Btn7=1 ;Continuous (not 2-tone) mode? IF.Btn0=3 ;SWEEP mode? UZ=UZ-1 ;Countdown to mtr update IF.UZ=<1 ;Countdown done? S=Posn?D / SmplRate ;Secs since (re)start L=QN * C ;Time for one sweep R=S % L ;Time into current sweep O=R * log2(W) / L ;Octaves into sweep F=2^O * Ctrl0 ;Current sweep freq ENDIF. ELSE. ;Else non-Sweep mode F=Ctrl0 ;Constant freq ENDIF. IF.UZ=<1 ;Countdown done? Mtr0="N" +p6 + "Hz" +p16 + "Deg" ;Show Mtr header U0=Btn0 ;Fundamental button state IF.U0=!2 ;Not Fundamental ONLY? UI=Ctrl3 ;Total harmonics WHILE.UI=>0 ;Show each, count down UH=Buf0[10 + UI] ;Saved harmonic num IF.UH=>0 ;Harmonic present? X=F * UH ;Harmonic freq P=Buf0[30 + UI] ;Saved phase Mtr0=Mtr0 + n + UH + p4 + X + p15 + P ENDIF. UI=UI-1 ;Next-lower harmonic WEND. ;Do all harmonics ENDIF. IF.U0=3 ;SWEEP mode? U0=0 ;Fundamental off if so ENDIF. IF.U0=>0 ;Fundamental on? Mtr0=Mtr0 + n + "1" + p4 + F + p15 + "0.000" ELSE. ;Show in parens if not Mtr0=Mtr0 + n + "1" + p3 _ + "(" + F +")" + p15 + "0.000" ENDIF. IF.Buf0[53]=>0 ;Crest factor ready? Mtr0=Mtr0 +n + " CF " + Buf0[53] + " dB" ;Show it ENDIF. UZ=10 ;Reset mtr update counter ENDIF. ELSE. ;Show 2-tone IF.(Btn0-3) || !UZ=0 ;STEP mode but not UZ=0 forced? S=Posn?D / SmplRate ;Seconds since (re)start QC=int(S / C) ;2-tone pairs done IF.QC=>UC ;Change since last update? UZ=0 ;Don't repeat UC=QC ;Update for change test L=QN + 1 ;Freq steps, incl start R=UC % L ;Step number in cycle O=2^(R * log2(W) / QN) ;Octave F=O * Ctrl0 ;Current A fund freq E=O * B ;B fundamental freq ELSE. ;Else no change UZ=10 ;Prevent update here ENDIF. ELSE. ;Non-STEP or forced update F=Ctrl0 ;Base A fundamental E=B ;Base B fundamental ENDIF. UG=0 ;Assume no show yet IF.UZ=<1 ;Countdown done? IF.Btn0=<2 ;If so, is Fund OFF or ON? IF.Buf0[50]=>0 ;CF value ready? UG=1 ;Show if so ENDIF. ELSE. ;Else if Fund ONLY or STEP UG=1 ;Always show ENDIF. ENDIF. IF.UG=1 ;Show values now? UZ=10 ;Prevent repeat update Mtr0="N" +p6 + "Hz" +p16 + "Deg" ;Show header IF.Btn0=2 ;Fundamentals ONLY? Mtr0=Mtr0 + n + "1" + QA(A) + p3 + F + p15 _ + "0.000" + n + n + "1" + QB(A) + p3 + E + p15 + "0.000" ELSE. ;Else show harmonics UI=Ctrl3 ;A from top down WHILE.UI=>0 UH=Buf0[20 + UI] ;Saved A harmonic # IF.UH=>0 ;Harmonic present? X=F * UH ;Harmonic freq Mtr0=Mtr0 + n + UH + QA(A) + p4 _ ;Show harm # + X + p15 + Buf0[40 + UI] ;Freq and phase ENDIF. UI=UI-1 ;Next-lower harmonic WEND. ;Do all harmonics U0=0 ;Assume no fundamental IF.Btn0=1 ;Fundamental ON? IF.Ctrl3=<4 ;Less than 4 harms? U0=1 ;Show w/o () ENDIF. ENDIF. IF.U0=1 ;Show fundamental Mtr0=Mtr0 + n + "1" + QA(A) + p4 + F _ + p15 + Buf0[40] +n ;Incl phase ELSE. ;Fundamental with () Mtr0=Mtr0 + n + "1" + QA(A) + p3 _ + "(" + F +")" + p15 + Buf0[40] +n ENDIF. IF.Buf0[51]=>0 ;Crest factor A ready? Mtr0=Mtr0 +" CF " + Buf0[51] + " dB" +n ;Show it ENDIF. UI=Ctrl3 ;B from top down WHILE.UI=>0 UH=Buf0[25 + UI] ;Saved B harmonic # IF.UH=>0 ;Harmonic present? X=E * UH ;Harmonic freq Mtr0=Mtr0 +n + UH + QB(A) + p4 _ ;Show harm # + X + p15 + Buf0[45 + UI] ;Freq and phase ENDIF. UI=UI-1 ;Next-lower harmonic WEND. ;Do all harmonics IF.Btn0=1 ;Fundamental ON? Mtr0=Mtr0 + n + "1" + QB(A) + p4 _ ;Show it + E + p15 + Buf0[45] ;Incl phase ELSE. ;Else show fund in () Mtr0=Mtr0 + n + "1" + QB(A) + p3 _ + "(" + E +")" + p15 + Buf0[45] ENDIF. IF.Buf0[52]=>0 ;Crest factor B ready? Mtr0=Mtr0 +n + " CF " + Buf0[52] + " dB" ;Show it ENDIF. ENDIF. ENDIF. ENDIF. ENDIF.
_Miss_Fund_Crest Macro Listing:
;<Help=H4913 IF.Buf0[50]=<2 ;Waiting for crest factor update? IF.Btn0=<2 ;Only for Fund OFF or ON IF.Btn7=1 ;Continuous Tone? UT=SmplRate / Ctrl0 ;Fundamental period @_Miss_Fund_CF_Core ;Compute CF Buf0[53]=V ;Store Cont CF Buf0[50]=3 ;Status = Cont CF done UZ=0 ;Force _Mtr update @_Miss_Fund_Mtr ELSE. ;Else Two-Tone S=Posn?D / SmplRate ;Seconds since (re)start Q=S % C ;Secs into this cycle IF.Buf0[50]=0 ;Waiting for A CF? IF.Q=>R ;Done with A Rise? IF.Q=<R + H - 1024 / SmplRate ;Before A High end? UT=SmplRate / Ctrl0 ;Fund A period @_Miss_Fund_CF_Core ;Get CF Buf0[51]=V ;Store A CF Buf0[50]=1 ;Status = A CF done UZ=0 ;Force _Mtr update @_Miss_Fund_Mtr ENDIF. ENDIF. ELSE. ;Else waiting for B CF IF.Q=>R+H+R+G+R ;Done with B Rise? IF.Q=<R+H+R+G+R+H - 1024/SmplRate ;Before B High end? UT=SmplRate / Buf0[19] ;Fund B period @_Miss_Fund_CF_Core ;Get CF Buf0[52]=V ;Store B CF Buf0[50]=2 ;Status = B CF done UZ=0 ;Force _Mtr update @_Miss_Fund_Mtr ENDIF. ENDIF. ENDIF. ENDIF. ENDIF. ENDIF.
_Miss_Fund_CF_Core Macro Listing:
;<Help=H4913 IF.Btn6=0 ;Only for waveform display Uc=Ch ;Save current channel during task Ch=1 ;Set to 1 for BwSig on Buf1 Buf1="<=W2" ;Copy Left Out waveform to Buf1 V=BwSig(0,UT) ;Get RMS over period UT UQ=Buf1?p ;Pos peak QQ=abs(Buf1?n) ;Abs of neg peak IF.QQ=>UQ ;Neg larger? UQ=QQ ;UQ = largest ENDIF. V=20 * log10(UQ/V) ;Peak/RMS ratio, as dB Ch=Uc ;Restore channel before task exit ELSE. V=0 ;No value if not waveform display ENDIF.
See also Auditory Phenomena and Experiments, Macro Examples and Mini-Apps
- Back to Sound Card Audible Phase Demonstration
- Ahead to Zwicker Tones
- Daqarta Help Contents
- Daqarta Help Index
- Daqarta Downloads
- Daqarta Home Page
- Purchase Daqarta
Questions? Comments? Contact us!
We respond to ALL inquiries, typically within 24 hrs.INTERSTELLAR RESEARCH:
Over 35 Years of Innovative Instrumentation
© Copyright 2007 - 2023 by Interstellar Research
All rights reserved