![[LogoShip]](logo5.png)
Software for Windows
Science with your Sound Card!
Spectral Averaging for Pre-Trigger Correlation
by Bob Masta
Interstellar Research
Previous Next
Last time, we discussed synchronous waveform averaging and pre-trigger correlation. That technique is a tool to help identify an unknown stimulus that is causing a response in your system. A typical application is where the input to the system contains many uncontrolled components, and you want to isolate the one that is actually provoking the response... say, a malfunction in a piece of equipment that you suspect is due to vibrations from nearby machinery.
The basic idea is that the system response is used to provide a trigger for the waveform averager, which has been continuously monitoring the system input and storing that signal to a circulating data buffer. When the trigger arrives, the averager reaches back into the buffer to extract a selected portion of the signal that arrived before the trigger. Averaging over many triggers, you can see if anything in that selected stretch of pre-trigger time is correlated with the subsequent arrival of the trigger. If so, it becomes a likely suspect as the direct or indirect cause of that trigger.
But we noted that this basic reverse correlation method is limited to revealing potential stimuli that are particular waveforms. It doesn't much matter what sort of waveform it is, be it tone burst, spike, or complex transient, but it must always appear with the same alignment before the trigger. Otherwise, it will not build up in the average: Misaligned peaks may be added to dips, causing cancellation instead of reinforcement.
Yet some systems respond to energy at particular frequencies without regard to phase. Consider a simple tone-signalling system: Tones are selected by bandpass filters and rectified to extract only their envelopes, discarding all phase information. Two tones could be 180 degrees out of phase, yet be equally effective at producing a response. Waveform averaging would not be able to extract the effective stimulus tones from a background of competing candidates: All would be averaged to zero since they were not phase-synchronous with the response.
However, there is a way to apply the general reverse correlation technique for frequencies instead of waveforms, by using spectrum averaging instead of waveform averaging. The basic acquisition system still acquires a set of data points that precede the trigger event, but they are not summed time-point by time-point into the averager array. Instead, a Fast Fourier Transform (FFT) is applied to each data set, and the resultant magnitude or power is summed, frequency by frequency, into the array. After dividing each array position by the total frames, the result is the average spectrum of the input.
Spectral averaging is very different from waveform averaging. It is most definitely not equivalent to the spectrum of an averaged waveform. For example, the spectrum average does nothing to reduce broadband noise; instead, it just yields the average noise level. Consider that a noise source may have more-or-less constant energy within any given analysis bandwidth, but the waveform certainly isn't constant and in fact typically averages toward zero.
Figure 1 shows this graphically. The yellow trace is the unaveraged spectrum of a 2 kHz tone in a rather noisy background. The light blue trace shows the average of 64 spectra, with the tone moved to 3 kHz for clarity. The average noise level at each analysis frequency is around -42 dB. The red trace shows the spectrum of a 64-frame waveform average, synchronous with the tone (now at 1 kHz). The noise level has been reduced by about 18 dB, as predicted by theory (3 dB reduction per frame-doubling).
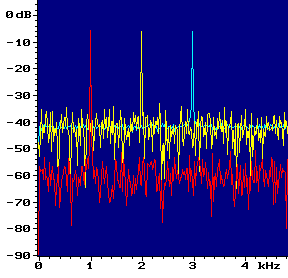
Fig. 1: Waveform vs Spectral Averaging
Since spectral averaging doesn't reduce background noise, as waveform averaging does, it can only work for reverse correlation if the unknown stimulus signal is larger than the average noise floor. That floor includes not only conventional broadband noise, but also interfering signals that might be present during the pre-trigger interval. In this application, any frequency components that are not present in the data before every trigger tend to be diminished by averaging, while those that are always present are enhanced... whether they are the ones we seek or not.
The magnitude or power spectral average will thus show the frequencies that are most correlated with the trigger event, without regard to phase. But what about those frequencies that were there all along, as part of the background, but have nothing to do with the response? To eliminate those you need to run a second average with the triggering set to "off" or "free-run", which effectively uncorrelates everything. Subtracting this background spectrum from the correlated spectrum will then reveal the potential stimulus frequencies.
Note another important difference compared to waveform reverse correlation: The spectral average is blind to the relative timing of any events that happen within the data interval used for each FFT. Suppose you sample the input data at 10240 samples per second (Fs), and take the FFT of the 1024 samples (N) preceding the trigger. That gives you the spectrum corresponding to a particular span of time N / Fs, or 0.10 second in this case.
Now suppose that the unknown stimulus is a tone burst that lasts only 0.025 seconds, or 256 samples. That burst could appear anywhere within the 0.10-second interval and it would produce exactly the same spectrum. So, since the precise timing of the stimulus before the trigger is unknown, the "wider net" of a large FFT size is helpful in capturing it.
The extra width does make it more likely to capture extraneous transients, however. Imagine a situation where the background contains bursts of some non-stimulus frequency at a rate that exceeds 10 per second. That means that every 1024-sample FFT will always see at least one of these uncorrelated bursts, so they will build up in the average along with the true correlated signal. That's why it is necessary to subtract the averaged uncorrelated background spectrum.
As with waveform averaging for reverse correlation, it's helpful to have some idea of where in time to look for the potential stimulus. The delay between the appearance of a stimulus and the subsequent response of the system under test will depend upon the nature of that system. If you know the internal time constants of the system, that may help get you started. Otherwise, if you can't think of any reason why there should be time lags, start with the pre-trigger delay set to view the N samples immediately before the trigger.
Once a suspect frequency is identified, you can opt to close in on the timing, if desired. To do this, you can try smaller FFT sizes in a binary search pattern: If the stimulus appears in a 1024-sample FFT, use a 512-sample FFT with the same pre-trigger delay to check the first half of the 1024 samples, and if you find nothing you can use a shorter delay to look at the second half. Or, if you get a partial response, the stimulus burst may have been straddling the middle of the interval.
Just recognize that when you cut the FFT size in half, you also cut the frequency resolution in half. This might cause a problem if there is an uncorrelated frequency near the stimulus you are seeking, since the two will tend to merge into a single peak. On the other hand, if the interfering signal is a burst, it will be less likely to land in the smaller FFT size. At some lower limit, however, you will be better off keeping the FFT size fixed and scanning the pre-trigger delay time to find the beginning and ending of the stimulus burst.
Hopefully, though, just identifying the frequency and a rough time interval will allow you to identify the stimulus. If you are looking for nearby machine vibrations that are bothering your equipment, you can compare with the spectra of indivdual machines, or possibly deduce their typical frequencies from RPMs and the number of gear teeth.
But what if the effective stimulus is not a particular frequency or set of frequencies, but a particular sequence of frequencies? We've seen how difficult it is to get timing information from a spectral average: If it shows two frequency peaks that were not present in the background, you don't know whether they were both present simultaneously, or whether one preceded the other. What if the order of presentation is important?
Once again, you could use a shorter spectral analysis window and move it to progressively earlier times before the trigger, possibly in a binary search. Your goal would be to find two separate time intervals, each of which shows only one of the two frequencies.
This is simply a matter of adjusting the pre-trigger delay and the FFT size, but note that if each spectral average requires many frames, you could be faced with a lot of runs for the whole analysis. If that is the case, a better way to do this task may be to record a resonably long time record before each trigger, and store a large number of these records separately, without any averaging. Then you will need to do the spectral averaging off-line, using custom software.
The ideal in such a case would be some sort of averaged spectrogram. Spectrograms are the most common form of joint time-frequency analysis (JTFA), and they can achieve fairly good temporal resolution by sliding the FFT window along in tiny steps. The fact that such software isn't readily available with any kind of averaging or pre-triggering provisions is probably a good indication that such extremes are rarely needed.
Fortunately, the majority of jobs require nothing more than simple waveform or spectral averaging, which you can get from ready-to-run software like the author's Daqarta for Windows software that uses your Windows sound card as a data acquisition system.
All Daqarta features are free to use for 30 days or 30 sessions, after which it becomes a freeware signal generator... with full analysis capabilities. (Only the sound card inputs are ignored.)
Daqarta can provide pre-trigger (or post-trigger) delays of more than 30000 samples, which is probably all that most engineers will need for sucessful implementation of the reverse correlation technique. Daqarta also has real-time and post-processing spectrogram capabilities, but if you think you are a candidate for averaged spectrogram reverse correlation, you'll still need custom software.
Previous Next
Features:
Oscilloscope
Spectrum Analyzer
8-Channel
Signal Generator
(Absolutely FREE!)
Spectrogram
Pitch Tracker
Pitch-to-MIDI
DaqMusiq Generator
(Free Music... Forever!)
Engine Simulator
LCR Meter
Remote Operation
DC Measurements
True RMS Voltmeter
Sound Level Meter
Frequency Counter
Period
Event
Spectral Event
Temperature
Pressure
MHz Frequencies
Data Logger
Waveform Averager
Histogram
Post-Stimulus Time
Histogram (PSTH)
THD Meter
IMD Meter
Precision Phase Meter
Pulse Meter
Macro System
Multi-Trace Arrays
Trigger Controls
Auto-Calibration
Spectral Peak Track
Spectrum Limit Testing
Direct-to-Disk Recording
Accessibility
Data Logger
Waveform Averager
Histogram
Post-Stimulus Time
Histogram (PSTH)
THD Meter
IMD Meter
Precision Phase Meter
Pulse Meter
Macro System
Multi-Trace Arrays
Trigger Controls
Auto-Calibration
Spectral Peak Track
Spectrum Limit Testing
Direct-to-Disk Recording
Accessibility
Applications:
Frequency response
Distortion measurement
Speech and music
Microphone calibration
Loudspeaker test
Auditory phenomena
Musical instrument tuning
Animal sound
Evoked potentials
Rotating machinery
Automotive
Product test
Contact us about
your application!
Questions? Comments? Contact us!
We respond to ALL inquiries, typically within 24 hrs.INTERSTELLAR RESEARCH:
Over 35 Years of Innovative Instrumentation
© Copyright 2007 - 2023 by Interstellar Research
All rights reserved