Dither Tricks

by Bob Masta
Interstellar Research

As we saw last time, dither can increase analog-to-digital converter (ADC) resolution for repetitive inputs. It does this by adding a small offset to the input signal, which is varied over a range at least equal to the least significant bit (LSB) of the converter. The LSB will toggle on or off in proportion to the amount of time the sum is above or below its threshold. By synchronously averaging many repetitions, the value of the input signal may be determined with a resolution proportional to the number of possible dither values and/or number of repetitions averaged.

Normally, the dither comes from a broadband noise source, although some input signals may have enough inherent noise to provide self-dither. Either way, the resultant input is noisy. Although synchronous waveform averaging will reduce that noise at the same time it increases the resolution, the noise doesn't go down as fast as the resolution goes up: Doubling the number of repetitions averaged will double the resolution, but it only reduces the noise by 3 dB. So if noise is added to increase resolution, it will also increase the noise in the final result.

But that assumes that the dither noise is uncorrelated with the averaging process. Under some circumstances it's possible to beat the odds and increase resolution without any noise penalty. The simplest conceptual approach, which is rarely used, is DC dither.

This method requires that the DC level be changed between repetitions of the input wave. The easiest way to achieve this is to have the averager increment a digital-to-analog converter ( DAC ) value after each input repetition, before it begins waiting for the next repetition sync. Before the DAC output is added to the input, it must be attenuated such that its total stepped range will traverse only +/- 1/2 LSB of the ADC during the desired number of repetitions. Figure 1 shows a typical setup:

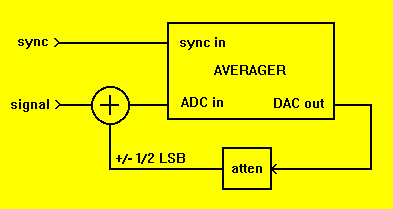
Fig. 1: DC Dither Setup

For example, if each attenuated DAC step is 1/256 LSB, then averaging 256 repetitions will give a 256-times increase in resolution, or 8 additional bits. There will be no noise added by this process: The ADC sees only the original signal, plus a DC component with an average value of zero.

The author has used this trick to extend the resolution of a 12-bit data acquisition board, used with a wide dynamic range laser vibrometer to monitor the auditory mechanics of a rodent’s ear. The dynamic range of the response greatly exceeded the 1-in-4096 resolution (72 dB) of the 12-bit system. A spare 12-bit DAC output on the acquisition board was used to provide the DC steps, with its full-scale output scaled to +/- 1/2 LSB of the ADC. By changing the step size and number of repetitions, the resolution could be increased by up to 12 bits. In practice, only 16 to 256 repetitions were used, adding 4 to 8 bits of resolution for an effective total of 16 to 20 bits.

With DC dither, all samples of the input signal receive the same added value on any given averager frame, and over the total number of repetitions they all see a staircase of values from the DAC. This technique requires that the ADC respond down to DC, of course, but the same idea will work in an AC-coupled system (like a sound card) as long as the same set of values are ultimately applied to each data sample. The key here is that the dither values must be correlated with sample position.

You could imagine a separate staircase generator for each sample position, each at a different phase. The DAC would need to output the appropriate value synchronously for each sample, rather than just one value per frame. DAC settling time and ADC setup time would need to be observed. Each sample would still see exactly the same overall set of values, only now each staircase would be wrapped at an arbitrary point. The overall dither would thus become an AC signal that the system could handle.

Furthermore, as long as you use the same set of values, there is no reason they need to be in any particular sequence; a pseudo-random sequence would give exactly the same result. The sequence could be stored in a circular lookup table, and each successive sample in any frame would get the next value from the sequence. At the end of each frame, the table pointer must be advanced so that each sample position sees all table values over the course of the repetitions.

To add 8 bits of resolution, for example, you need a table of all values from 0 through 255. To insure that each value appears exactly once, an 8-bit Maximum Length Sequence (MLS) generator could be used. However, note that an MLS sequence will give values from 1 to 255; the 0 value is always excluded. So, just append a 0 in the final table position... it's as good a place for it as any. Since the table size will be a power of 2, you can make it circular by ANDing the index pointer with the appropriate mask value, in this case 255, before adding it to the table base pointer to fetch a value.

This correlated dither technique requires a fair amount of sophistication, including interleaved DAC and ADC samples as well as table handling. The DC technique is much simpler, but still requires a DAC and a way to step it after each frame. Isn't there something simpler, something you could have in your bag of tricks for those occasions when you just need to squeeze a few more bits from a test setup? Of course, you could add noise... if you had a noise generator handy, and didn't mind the added noise in the final average. But a standard function generator is usually more readily available, and it turns out it's usually a better choice as well.

The basic idea is to make sure that the LSB of the ADC is always exercised adequately. It doesn't matter whether the dither signal is at DC, spread throughout the spectrum like wideband noise, or at a discrete frequency, as long as that frequency it is not correlated with the desired signal sync. In other words, when you view the instantaneous trace on the signal averager, you want the desired signal to appear stationary, while the dither rolls through it asynchronously. The frequency separation of the dither from the signal is not the issue here, only the synchrony.

Start with a high dither level for easy setup, and tweak its frequency if it looks too stationary relative to the signal sync. In this respect, it is much easier to adjust a low dither frequency for maximum asynchrony than a high one. Best results are often obtained when the dither frequency is near an odd multiple of the sync rate, since alternating frames catch the dither about 180 degrees out of phase, giving an "eye" pattern on the trace.

Next, reduce the dither level to zero and look only at the desired signal. Boost the trace magnification until you can clearly see the quantization steps of the ADC. You may wish to reduce the input signal level temporarily to make this easier. Otherwise, at the high magnifications needed to see the steps, most of the signal may be off-screen and the on-screen portions may be nothing but steep slopes that don't show steps very well.

Now raise the dither level until you see some action. If the dither frequency is much higher than the signal frequency, it will appear as a forest of "grass" growing out of each ADC step. If the frequency is much lower, the signal trace will ride up and down on the dither. You want either the grass level or the vertical ride distance to cover at least two ADC steps. Average a number of frames and see what happens. If the average still shows nonlinearities or other remnants of the original steps, try boosting the dither level some more.

Figure 2 shows 64-frame averages of the same signal with several different dither conditions. The ADC used here is an inexpensive sound card running in 8-bit mode to deliberately give low resolution for this demonstration. The signal, one cycle of a 200 Hz sine from the sound card's on-board synthesizer, is at such a low level that with no dither (bottom trace, in yellow) the quantization steps are clearly seen. (The steps appear rounded due to the effects of averaging on a slight frame-to-frame sync jitter.)

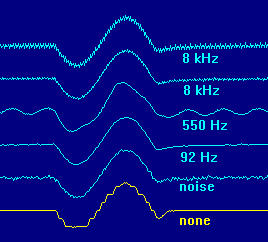
Fig. 2: Dither Comparison

The next trace up from the bottom shows the results of wideband noise dither. Compare it to the much quieter trace above it, which used 92 Hz sine wave dither. This improvement is because 92 Hz is near an odd multiple of the sync rate, so alternating frames tend to cancel. Of course, if it were an exact odd multiple, the dither effect would be subverted, especially at the nodes of the dither "eye" pattern. This was a deliberate attempt to hit the multiple, but without phase locking between the signal and dither sources it quickly drifted enough to insure a good dither effect anyway.

Above the 92 Hz trace is one that used 550 Hz dither, which was deliberately set near an even multiple of the sync rate to try to get a stable dither trace. Thus, even though there was enough drift to give a good dither effect, it shows poor cancellation. This is a particularly bad case, since it is hard to distinguish the dither from the signal. If a very low or high dither frequency had been used with this signal, there would have been less possibility for confusion, even with inadequate cancellation.

Finally, the top two traces used an 8 kHz dither source. They were both acquired identically, and are examples of typical residuals from high frequency dither; better or worse results are possible. During the averaging operations, the running display showed the residual waxing and waning as the dither drifted in and out of phase relative to the signal sync. The relative drift is much greater at this high frequency, so the results tend to be more variable. But note that there is no danger of confusion of the residual with the signal, as there was in the 550 Hz case.

The astute reader may be wondering why sinusoidal dither was used here, since the previous column indicated that a uniform distribution of dither values over the LSB range is the ideal. Wouldn't a triangle wave be better? In theory, perhaps, but in reality this is overridden by other factors. The prior column discussed noise dither, and the noise is eliminated only slowly by averaging. So it made sense to keep its level as low as possible, which would require a uniform distribution over the LSB range. It was noted that other noise distributions would require higher levels, and the same is true here for other waveforms than triangular.

Moreover, with a continuous wave as a dither source, it is usually easy to adjust for a partial cancellation effect that doesn't apply with random noise, so a larger dither level isn’t a particular problem here. However, at low dither frequencies there is an advantage to sine waves in that any residual tends to be a sine wave also, and that may be less objectionable in the final result than a residual from a triangle.

Nevertheless, triangles can be made to work perfectly well. In fact, even square waves can do a decent job under some conditions. How can this be? With only two discrete levels, surely there can be no dither effect... can there? Actually, this only works well on sloping portions of the signal, where the square wave edges sweep over the slope due to asynchrony. It has problems with peaks and flat portions, but it is still a considerable improvement over no dither at all.

The next column will discuss the use of various forms of dither to provide high resolution in the most extreme case of all: A one-bit ADC, which can be easily rigged from any digital input (like a parallel port) and run at very high sample rates on an old DOS system.

Until then, you can try some of the above dither tricks using the author's Daqarta for Windows software, which turns your Windows sound card into a data acquisition system. It has extensive built-in signal and noise generation options, and you can average the raw data directly without needing any external hardware connections.

All Daqarta features are free to use for 30 days or 30 sessions, after which it becomes a freeware signal generator... with full analysis capabilities. (Only the sound card inputs are ignored.)