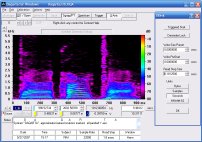
Sound Card Spectrum X-log Toggle

Controls: Spectrum Dialog >> X-log
Macro: Xlog

This button also appears as the X-log Spect button in the X-Axis Control Dialog. Alternatively, you can toggle X-log mode via ALT+SHIFT+X whenever Spectrum mode is active, regardless of which dialog is visible.

This option allows the Spectrum X axis to be shown with logarithmic scaling. Combined with the Y-log power spectrum mode to get a log-log display, this is a standard method for viewing scientific and engineering data of all sorts, especially where wide ranges must be shown in a single view.

Since this mode just replots the same data with a different spacing, you will note that low-frequency points are far apart and high-frequency parts are close together or even overlapping.

Many phenomena that show an exponential response on a linear scale become linear on a log-log scale. A typical example of this is the behavior of a simple low-pass filter: Above its cutoff frequency, the output falls off proportional to the inverse of frequency. In log terms, this halving for each frequency doubling is usually expressed as a slope of "6 dB per octave" or the equivalent "20 dB per decade". For a filter whose response falls as the inverse square of frequency, the log-log slope would be 12 dB per octave, and for the inverse cube it would be 18 dB per octave.

The log-log slope, properly interpreted, is thus a measure of the mathematical "degree" of the underlying equation of a simple system, be it mechanical, electrical, or whatever. Although there are many pitfalls to using this idea to analyze an unknown system, it can be very useful when carefully applied to well-behaved systems.

Another example where a log-log plot is useful is in viewing a pink noise source. In log-log mode, the spectrum (after enough averaging), appears as a straight line that shows a -3 dB / Octave downward tilt that is characterstic of pink noise.

Note that if you use the X-Axis eXpand function while in X-log mode, the settings are kept separate from those of linear X-axis mode.

Macro Notes:

Xlog=1 sets Spectrum X-log mode, Xlog=0 restores linear X axis, and Xlog=x toggles between them.

See also Spectrum Control Dialog